Seminar -
Geometric formulations of inviscid fluids and their discretization
- OvGU - 2019
Lecturer: Jan Heiland, Christian Lessig
This seminar in the LSF
| Day | Time | Place |
|---|---|---|
| Wednesday | 11:00-13:00 | G2-20 |
Consultation hours: Please make an appointment by email.
Introduction
Curiously, the geometrical description that is closely connected with Hamilton’s principle or Langrange’s variational formulation and that is commonly used to model mechanical systems like a pendulum also applies to the equations of fluid motion.
Standard numerical methods for continuous dynamical systems destroy the geometric structures of these systems. Practically, this means that physical invariants like the energy or the momentum are lost in the discrete model.
In this seminar, we will study the systematic construction of structure preserving methods that remedy this deficiency. After studying in detail the pendulum to introduce the mathematical and numerical formulation, we will consider the Euler equation for ideal fluids, a system that exhibits both the elegance and complexity of the subject.
Later on, we will address both classical and recent related research topics.
As a motivating example we will consider the time integration for a simple pendulum and how its energy is preserved during the time stepping. For that we compare the symplectic Euler scheme (which is of 1st order) to the Runge-Kutta scheme (which is of 4th order). Please have a look at the basic python implementation.
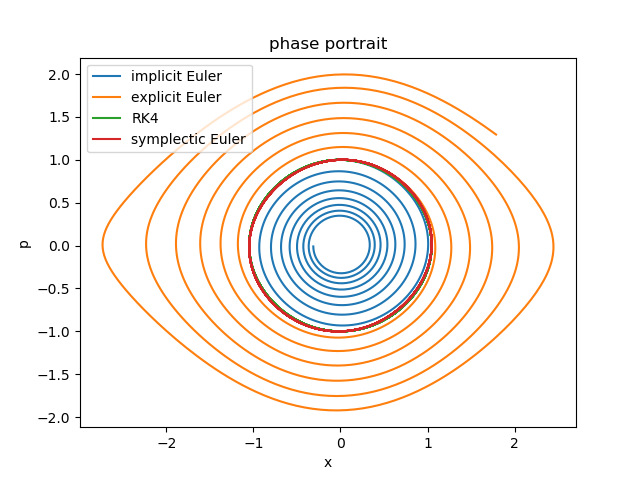
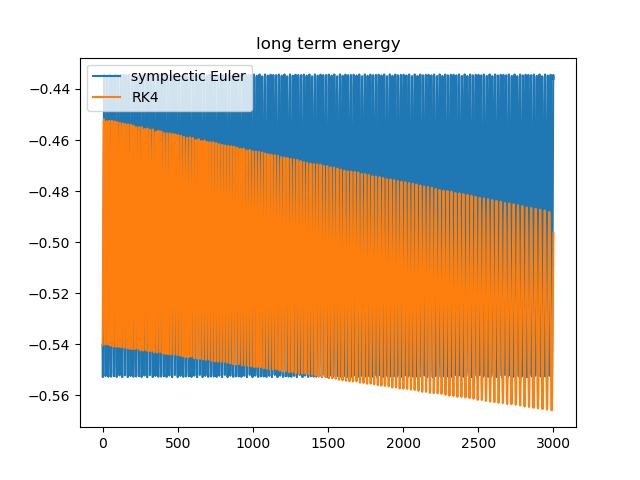
Topics
Variational formulation of ideal fluid
Develop the variational formulation of ideal fluid dynamics, possibly including the general perspective of Euler-Poincare reduction.
![]() V. I. Arnold, Mathematical Methods of Classical Mechanics, Second. ed. Springer, 1989 (Appendix A).
V. I. Arnold, Mathematical Methods of Classical Mechanics, Second. ed. Springer, 1989 (Appendix A).
![]() J. E. Marsden and T. S. Ratiu, Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, Third ed. New York: Springer-Verlag, 1999.
J. E. Marsden and T. S. Ratiu, Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, Third ed. New York: Springer-Verlag, 1999.
Hamiltonian formulation of ideal fluid
Develop the Hamiltonian formulation of ideal fluid dynamics, including conserved quantities in 2D and 3D.
![]() J. E. Marsden and A. Weinstein, Coadjoint orbits, vortices, and Clebsch variables for incompressible fluids, Phys. D Nonlinear Phenom., vol. 7, no. 1–3, pp. 305–323, May 1983. [pdf]
J. E. Marsden and A. Weinstein, Coadjoint orbits, vortices, and Clebsch variables for incompressible fluids, Phys. D Nonlinear Phenom., vol. 7, no. 1–3, pp. 305–323, May 1983. [pdf]
![]() V. I. Arnold and B. A. Khesin, Topological Methods in Hydrodynamics. New York: Springer, 1998.
V. I. Arnold and B. A. Khesin, Topological Methods in Hydrodynamics. New York: Springer, 1998.
Algebraic, structure preserving numerical method for ideal fluid dynamics
Theory: Develop the discretization of 2D ideal fluid dynamics proposed by Zeitlin based on the work by Hoppe.
Implementation: Develop an implementation of the algorithm proposed by Zeitlin, as done by McLachlan.
![]() V. Y. Zeitlin, Finite-mode analogs of 2D ideal hydrodynamics: Coadjoint orbits and local canonical structure, Phys. D Nonlinear Phenom., vol. 49, no. 3, pp. 353–362, Apr. 1991.
V. Y. Zeitlin, Finite-mode analogs of 2D ideal hydrodynamics: Coadjoint orbits and local canonical structure, Phys. D Nonlinear Phenom., vol. 49, no. 3, pp. 353–362, Apr. 1991.
![]() J. Hoppe, Diffeomorphism Groups, Quantization, and SU(∞), Int. J. Mod. Phys. A, vol. 04, no. 19, pp. 5235–5248, Nov. 1989.
J. Hoppe, Diffeomorphism Groups, Quantization, and SU(∞), Int. J. Mod. Phys. A, vol. 04, no. 19, pp. 5235–5248, Nov. 1989.
![]() S. J. Rankin, SU(∞) and the large-N limit, Ann. Phys. (N. Y)., vol. 218, no. 1, pp. 14–50, Aug. 1992.
S. J. Rankin, SU(∞) and the large-N limit, Ann. Phys. (N. Y)., vol. 218, no. 1, pp. 14–50, Aug. 1992.
![]() R. I. McLachlan, Explicit Lie-Poisson integration and the Euler equations, Phys. Rev. Lett., vol. 71, no. 19, pp. 3043–3046, Nov. 1993. [pdf]
R. I. McLachlan, Explicit Lie-Poisson integration and the Euler equations, Phys. Rev. Lett., vol. 71, no. 19, pp. 3043–3046, Nov. 1993. [pdf]
Madelung transform
Develop the Madelung transform as a hydrodynamical model for the Schrödinger equation, with an emphasis on the geometric perspective as a momentum map that connects it to compressible fluid dynamics.
Optional: Also develop the connection to the work by [Chern et al. 2016].
![]() D. Fusca, The Madelung transform as a momentum map, J. Geom. Mech., vol. 9, no. 2, pp. 157–165, 2017. [pdf]
D. Fusca, The Madelung transform as a momentum map, J. Geom. Mech., vol. 9, no. 2, pp. 157–165, 2017. [pdf]
![]() E. Madelung, Quantentheorie in hydrodynamischer Form, Zeitschrift für Phys., vol. 40, no. 3–4, pp. 322–326, Mar. 1927.
E. Madelung, Quantentheorie in hydrodynamischer Form, Zeitschrift für Phys., vol. 40, no. 3–4, pp. 322–326, Mar. 1927.
![]() E. Madelung, Eine anschauliche Deutung der Gleichung von Schrödinger, Naturwissenschaften, vol. 14, no. 45, pp. 1004–1004, Nov. 1926.
E. Madelung, Eine anschauliche Deutung der Gleichung von Schrödinger, Naturwissenschaften, vol. 14, no. 45, pp. 1004–1004, Nov. 1926.
![]() A. Chern, F. Knöppel, U. Pinkall, P. Schröder, and S. Weißmann, Schrödinger’s smoke, ACM Trans. Graph., vol. 35, no. 4, pp. 1–13, Jul. 2016.
A. Chern, F. Knöppel, U. Pinkall, P. Schröder, and S. Weißmann, Schrödinger’s smoke, ACM Trans. Graph., vol. 35, no. 4, pp. 1–13, Jul. 2016.
![]() M. Schönberg, On the hydrodynamical model of the quantum mechanics, Nuovo Cim., vol. 12, no. 1, pp. 103–133, Jul. 1954.
M. Schönberg, On the hydrodynamical model of the quantum mechanics, Nuovo Cim., vol. 12, no. 1, pp. 103–133, Jul. 1954.
Spectral, structure preserving integrator for ideal fluid dynamics
Develop an implementation of the algorithm proposed by Liu et al. [2015].
![]() B. Liu, G. Mason, J. Hodgson, Y. Tong, and M. Desbrun, Model-reduced variational fluid simulation, ACM Trans. Graph., vol. 34, no. 6, pp. 1–12, Oct. 2015.
B. Liu, G. Mason, J. Hodgson, Y. Tong, and M. Desbrun, Model-reduced variational fluid simulation, ACM Trans. Graph., vol. 34, no. 6, pp. 1–12, Oct. 2015.
![]() J. E. Marsden and A. Weinstein, Coadjoint orbits, vortices, and Clebsch variables for incompressible fluids, Phys. D Nonlinear Phenom., vol. 7, no. 1–3, pp. 305–323, May 1983. [pdf]
J. E. Marsden and A. Weinstein, Coadjoint orbits, vortices, and Clebsch variables for incompressible fluids, Phys. D Nonlinear Phenom., vol. 7, no. 1–3, pp. 305–323, May 1983. [pdf]
![]() T. de Witt, C. Lessig, and E. Fiume, Fluid Simulation Using Laplacian Eigenfunctions, ACM Trans. Graph., vol. 31, no. 1, pp. 1–11, Jan. 2012. [pdf]
T. de Witt, C. Lessig, and E. Fiume, Fluid Simulation Using Laplacian Eigenfunctions, ACM Trans. Graph., vol. 31, no. 1, pp. 1–11, Jan. 2012. [pdf]
Variational, structure preserving numerical integrator for arbitrary meshes
Theory: Develop the variational structure preserving integrator proposed by Pavlov et al. [2011], possibly including the extensions in Gawlik et al. [2011].
Implementation: Implement the algorithm presented by Mullen et al. (2D, on a regular grid or using PyDec).
![]() E. S. Gawlik, P. Mullen, D. Pavlov, J. E. Marsden, and M. Desbrun, Geometric, variational discretization of continuum theories, Phys. D Nonlinear Phenom., vol. 240, no. 21, pp. 1724–1760, Oct. 2011. [pdf]
E. S. Gawlik, P. Mullen, D. Pavlov, J. E. Marsden, and M. Desbrun, Geometric, variational discretization of continuum theories, Phys. D Nonlinear Phenom., vol. 240, no. 21, pp. 1724–1760, Oct. 2011. [pdf]
![]() D. Pavlov, P. Mullen, Y. Tong, E. Kanso, J. E. Marsden, and M. Desbrun, Structure-preserving discretization of incompressible fluids, Phys. D Nonlinear Phenom., vol. 240, no. 6, pp. 443–458, Mar. 2011.
D. Pavlov, P. Mullen, Y. Tong, E. Kanso, J. E. Marsden, and M. Desbrun, Structure-preserving discretization of incompressible fluids, Phys. D Nonlinear Phenom., vol. 240, no. 6, pp. 443–458, Mar. 2011.
![]() P. Mullen, K. Crane, D. Pavlov, Y. Tong, and M. Desbrun, Energy-Preserving Integrators for Fluid Animation, ACM Trans. Graph. (Proceedings SIGGRAPH 2009), vol. 28, no. 3, pp. 1–8, 2009.
P. Mullen, K. Crane, D. Pavlov, Y. Tong, and M. Desbrun, Energy-Preserving Integrators for Fluid Animation, ACM Trans. Graph. (Proceedings SIGGRAPH 2009), vol. 28, no. 3, pp. 1–8, 2009.
Vorticity-based, structure preserving discretization of fluids
Develop an implementation of the technique proposed by Elcott et al. [2007]
![]() S. Elcott, Y. Tong, E. Kanso, P. Schröder, and M. Desbrun, Stable, Circulation-Preserving, Simplicial Fluids, ACM Trans. Graph., vol. 26, no. 1, 2007. [pdf]
S. Elcott, Y. Tong, E. Kanso, P. Schröder, and M. Desbrun, Stable, Circulation-Preserving, Simplicial Fluids, ACM Trans. Graph., vol. 26, no. 1, 2007. [pdf]
General literature
![]() V. I. Arnold, Mathematical Methods of Classical Mechanics, Second. ed. Springer, 1989.
V. I. Arnold, Mathematical Methods of Classical Mechanics, Second. ed. Springer, 1989.
![]() J. E. Marsden, Lectures on Mechanics, Cambridge University Press, 1992.
J. E. Marsden, Lectures on Mechanics, Cambridge University Press, 1992.
![]() J. E. Marsden and T. S. Ratiu, Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, third ed., New York: Springer-Verlag, 1999.
J. E. Marsden and T. S. Ratiu, Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, third ed., New York: Springer-Verlag, 1999.
![]() D. D. Holm, T. Schmah, and C. Stoica, Geometric Mechanics and Symmetry: From Finite to Infinite Dimensions, Oxford University Press, 2009.
D. D. Holm, T. Schmah, and C. Stoica, Geometric Mechanics and Symmetry: From Finite to Infinite Dimensions, Oxford University Press, 2009.
![]() Tudor Ratiu. A Crash Course in Geometric Mechanics, third cycle. Monastir (Tunisie), 2005
Tudor Ratiu. A Crash Course in Geometric Mechanics, third cycle. Monastir (Tunisie), 2005
![]() R. Abraham and J. E. Marsden, Foundations of Mechanics, second ed., Addison-Wesley Publishing Company, Inc., 1978.
R. Abraham and J. E. Marsden, Foundations of Mechanics, second ed., Addison-Wesley Publishing Company, Inc., 1978.
![]() J. E. Marsden, T. S. Ratiu, and R. Abraham, Manifolds, Tensor Analysis, and Applications, Third ed., New York: Springer-Verlag, 2004.
J. E. Marsden, T. S. Ratiu, and R. Abraham, Manifolds, Tensor Analysis, and Applications, Third ed., New York: Springer-Verlag, 2004.
![]() E. Hairer, C. Lubich, and G. Wanner, Geometric Numerical Integration, Second ed. Springer-Verlag, 2006.
E. Hairer, C. Lubich, and G. Wanner, Geometric Numerical Integration, Second ed. Springer-Verlag, 2006.
![]() J. E. Marsden and M. West, Discrete Mechanics and Variational Integrators, Acta Numer., vol. 10, pp. 357–515, 2001.
J. E. Marsden and M. West, Discrete Mechanics and Variational Integrators, Acta Numer., vol. 10, pp. 357–515, 2001.
![]() A. Stern and M. Desbrun, Discrete Geometric Mechanics for Variational Time Integrators, in SIGGRAPH ’06: ACM SIGGRAPH 2006 Courses., 2006.
A. Stern and M. Desbrun, Discrete Geometric Mechanics for Variational Time Integrators, in SIGGRAPH ’06: ACM SIGGRAPH 2006 Courses., 2006.