Vorlesung und Übungen zur Funktionentheorie - OvGU - 2017
Es gibt Prüfungstermine: 05., 15. und 28. März und 09. April. Wer es nicht schafft, sich in die Liste einzutragen, der meldet sich per Email.
Hier gibt’s die grundlegenden und aktuelle Informationen zur Vorlesung Funktionentheorie and der OvGU im Wintersemester 2017. Verantwortlich sind Jan Heiland and Steffen Werner.
| Tag | Zeit | Ort |
|---|---|---|
| Dienstag | 11:00-13:00 | G22A-119 |
| Donnerstag | 11:00-13:00 | G12-201 |
![]() Zu den Übungen.
Zu den Übungen.
Übersicht über die Vorlesung
- Historische Einführung und grundlegende Konzepte [Woche 1]
- Historischer Abriss und Anwendungen
- Literatur
- Grundlagen
- Differentiation im Komplexen
- Integration im Komplexen [Woche 8]
- Kurven und Kurvenintegrale
- Stammfunktionen [Woche 9]
- Wegunabhängigkeit
- Cauchy’s Integralsatz [Woche 10]
Übungen
| Date | Topic | Sheet |
|---|---|---|
| 26. Oktober | I - Komplexe Zahlen | blatt_01.pdf |
| 09. November | II - Potenzreihen und Sin/Cos/Exp
|
blatt_02.pdf |
| 23. November | III - Stetigkeit und Differenzierbarkeit | blatt_03.pdf |
| 7. Dezember | IV - Integration im Komplexen | blatt_04.pdf |
| 14. Dezember | V - Stammfunktionen | blatt_05.pdf |
| 18. Januar | VI - Integrale und Singularitäten | blatt_06.pdf |
| 25. Januar | VII - Definitionen und Beispiele | nur online |
Woche 1
Einführung
+++ Entdeckung/Entwicklung und Formalisierung der komplexen Zahlen +++ Mathematische Definition +++ Rechnen mit komplexen Zahlen +++ zurück zur Übersicht
Woche 2
+++ Polardarstellung +++ Potenzieren und Wurzel ziehen +++ (konvergente) Potenzreihen +++ zurück zur Übersicht
Woche 3
Übungsblatt 1 -- 26. Oktober
+++ Rechnen mit komplexen Zahlen +++ Wurzeln ziehen +++ Betragsungleichungen +++ zurück zur Übersicht
Woche 4
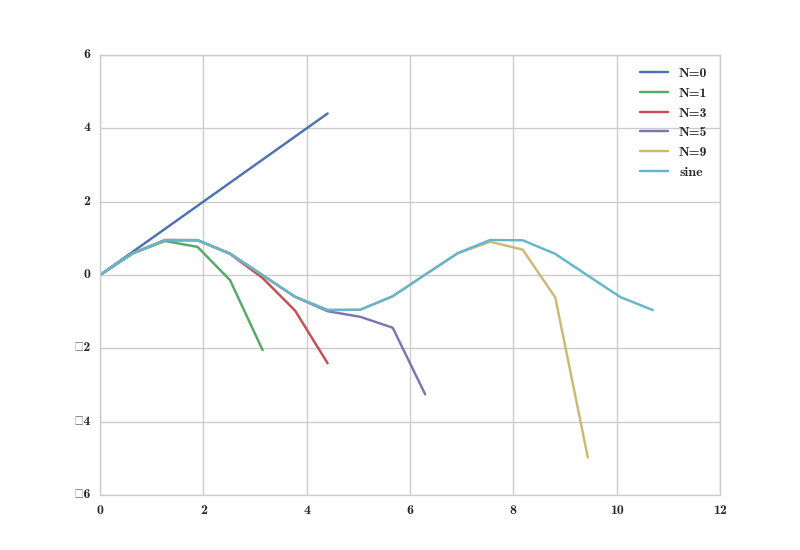
+++ Sinus, Cosinus und die Exponentialfunktion als Potenzreihen +++ Additionstheoreme +++ Approximation durch abgeschnittene Potenzreihen +++ ![]() Illustration –
Illustration – ![]() pythoncode +++ Stetigkeit und Darstellung komplexer Funktionen +++ zurück zur Übersicht
pythoncode +++ Stetigkeit und Darstellung komplexer Funktionen +++ zurück zur Übersicht
Woche 5
+++ Stetigkeit von Verküpfungen +++ Differenzierbarkeit und holomorphe Funktionen +++ Rechenregeln zur Ableitung +++ “holomorphe Funktionen sind beliebig oft differenzierbar” +++ zurück zur Übersicht
Übungsblatt 2 -- 09. November
+++ Potenzreihen +++ Exp/Sin/Cos +++ Exponentialgesetze und Additionstheoreme+++ zurück zur Übersicht
Woche 6
+++ Ableitung als Linearisierung +++ Herleitung der Cauchy-Riemann’schen Differentialgleichungen +++ Folgerungen aus den Cauchy-Riemann’schen Differentialgleichungen +++ zurück zur Übersicht
Woche 7
+++ Strecken- und Winkeltreue holomorpher Funktionen +++ Invertierbarkeit +++ zurück zur Übersicht
Übungsblatt 3 -- 23. November
+++ Komplexe Differenzierbarkeit +++ Cauchy-Riemann’sche Differentialgleichungen +++ Ableitung von Potenzreihen +++ zurück zur Übersicht
Woche 8
+++ Kurven in der komplexen Ebene +++ Parametrisierung und (stückweise Glattheit) +++ Integration entlang von Kurven +++ Bogenlänge +++ zurück zur Übersicht
Woche 9
+++ Stammfunktionen +++ Integral über geschlossene Kurven +++ Wegunabhängigkeit +++ zurück zur Übersicht
Übungsblatt 4 -- 7. Dezember
+++ Integal von Funktionen längs von Kurven +++ Parametrisierungsinvarianz ++ zurück zur Übersicht+
Woche 10
+++ Konvexe- und Sterngebiete +++ Cauchys Integralsatz +++ Cauchys Integralformel +++ zurück zur Übersicht
Übungsblatt 5 -- 14. Dezember
+++ Kettenregel +++ Stammfunktionen +++ Wegunabhängigkeit gdw. verschwindendes Integral über geschlossene Kurven +++ zurück zur Übersicht
Woche 11
+++ Folgerungen aus Cauchys Integralformel +++ Leibnizsche Regel +++ verallgemeinerte Integralformel Cauchys +++ zurück zur Übersicht
+++ ganze Funktionen +++ Fundamentalsatz der Algebra +++ zurück zur Übersicht
Woche 12
+++ analytische Funktionen +++ gleichmäßige Approximation +++ Potenzreihen revisited +++ zurück zur Übersicht
Woche 13
+++ Charakterisierung von isolierten Singularitäten +++ Laurent-Reihen +++ zurück zur Übersicht
Übungsblatt 6 -- 18. Januar
+++ Integral mit Singularitäten +++ Potenzreihenentwicklung +++ Singularitäten +++ zurück zur Übersicht
Woche 14
+++ Laurent-Reihen +++ Residuen +++ zurück zur Übersicht
Übung 7 -- 25. Januar
Man trage eine der folgenden Definitionen frei vor und erläutere sie mit Hilfe einer Illustration oder einem Beispiel.
- 1.1 imaginaere Einheit, komplexe Zahl, Gleichheit, Menge CC, Komplexe Ebene
- Konvergente Folge und Reihe
- Konvergenzbereich
- Exponentialfunktion, Sinus/Kosinus
- 1.8 Stetigkeit von Funktionen
- 2.1 Komplex differenzierbar
- 2.1.1 Holomorphe Funktion
- (2.6) Cauchy-Riemann Differentialgleichungen
- 3.1 Kurve ((stckw.) glatt)
- 3.2 Kurvenintegral
- 3.3 Stammfunktion
- (3.6 Gebiet)
- 3.17 ganze Funktion
- (4.1 glm. Konvergenz)
- (4.6 glm. Konvergenz bei Funktionenreihen)
- 5.1 punktierte Kreisscheibe
- 5.2 isolierte Singularitaet (hebbar, Pol, wesentlich)
- 5.7 Laurent-Reihe (Hauptteil, Regulaerteil)
- Konvergenzbereich der Laurent-Reihe
- 5.11 Residuum
Literatur
| Author | Titel | Kommentar |
|---|---|---|
| Herz, Andreas | Repetitorium Funktionentheorie | enthält alle Inhalte der Vorlesung – wenig Fließtext ++ viele Beispiele und durchgerechnete Übungsaufgaben |
| Jänich, Klaus | Funktionentheorie: eine Einführung | viel Text und viele Erklärungen ++ setzt Kenntnisse der komplexen Zahlen und der Differentialrechnung im Reellen voraus |