A benchmark for fluid rigid body interaction with standard CFD packages

Henry von Wahl & Thomas Richter & Jan Heiland

Christoph Lehrenfeld & Piotr Minakowski

GAMM CSE -- 21 November 2019

Introduction

What is a Benchmark

I haven't found a clear definition of what a benchmark is. However, here is what I think makes a numerical example a benchmark

  1. Common acceptance as a benchmark -- there are other publications that discuss the same setup.
  2. Practical relevance -- either in applications or as a testing field for numerical algorithms.
  3. Reliable reference data -- so that others can test their codes and methods against it.

What is a Benchmark

Basically, everything that would motivate a fellow researchers to use the provided setup and data to benchmark their code.

Why Benchmarks

Quantitative assessments, evaluate performance:

We know that this computation correct, but how efficient is it?

Examples:

Why Benchmarks

Qualitive assessments, evaluate confidence:

Are the computations correct?

Example: FEATFLOW CFD Benchmarking project

Note that:

The more complex the model is, the more necessary are benchmarks but the more difficult are benchmark definitions.

Fluid Structure Interaction

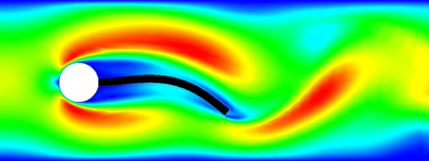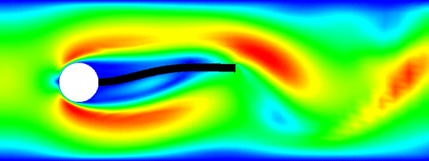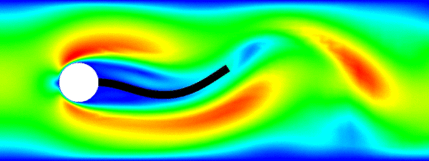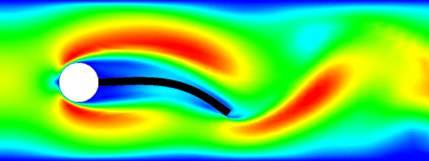
Example of a cylinder with a tail
Example of a cylinder with a tail
  • Changing domain.
  • Coupling of Models (and scales).

Our Benchmark

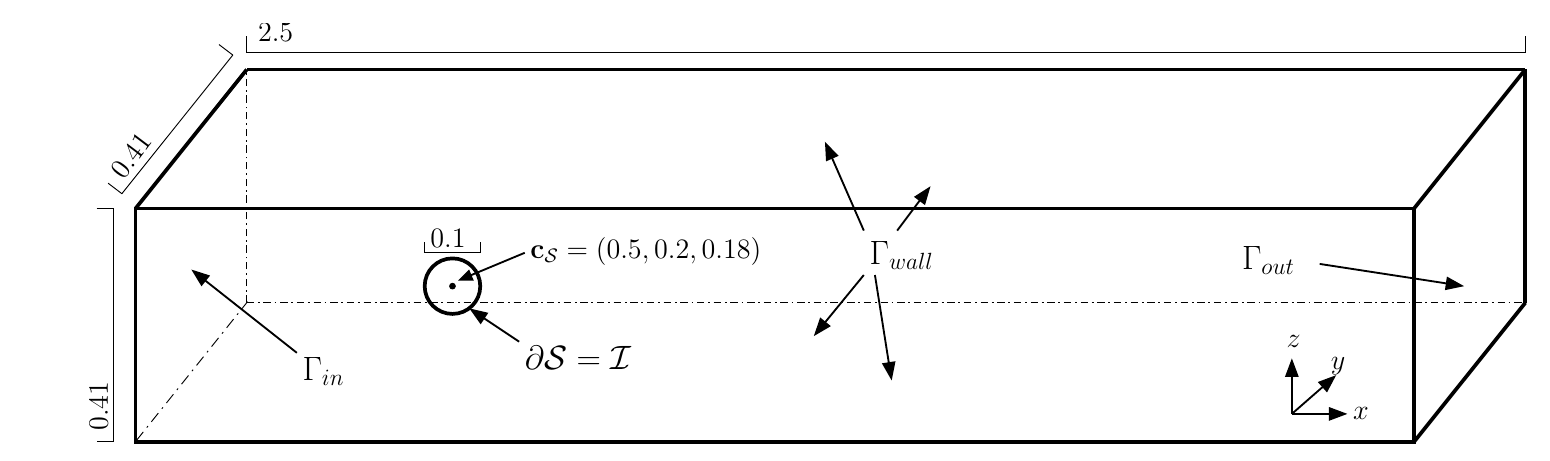
3D setup of the computational domain
3D setup of the computational domain

A freely rotating sphere with fixed center

  • The domain is fixed.
  • Can concentrate on the coupling of the models.
  • Accessible to standard CFD solvers.

We address (2.) and (3.) of the benchmark criteria

  • Relevant as a testing field for algorithms and
  • reliable test data.

(1.) General acceptance as a benchmark may come later.

The model

Verbose

  • A fluid flows through a channel with a sphere that can rotate freely.
  • The stresses at the sphere/fluid interface induce rotation.
  • The no-slip condition induces motion of the flow at the interface.

The flow

\[\begin{equation*} \rho_f\left(\partial_t v + (v \cdot\nabla)v \right) - \nabla \cdot \sigma(v ,p) = 0, \quad \nabla\cdot v = 0, \end{equation*}\] with the stress-tensor \[\begin{equation*} \sigma (v,p) = \rho _ f\nu\left( \nabla v+\nabla v^T \right) - p I \end{equation*}\] and with standard boundary conditions and in particular \[\begin{equation*} v = v_s, \quad \text{on } \mathcal I, \end{equation*}\]

where \(v_s\) is the solid's velocity at the fluid-solid interface.

The rigid body

\[\begin{equation*} J\partial_t\omega = \mathbf T \end{equation*}\] where \(J\) is the body's moment of inertia and \(\mathbf T\) is the total torque exerted onto the body by the fluid. \[\begin{equation*} \mathbf T = \int_{\mathcal I} (\mathbf x-\mathbf c)\times \left( \sigma( v,p )\mathbf n \right) ds \end{equation*}\]

with the body's centre of mass \(\mathbf c\).

Test Cases

Setups

  • 2D and 3D
  • stationary -- where there is no torque (low Re-number)
  • periodic -- a limit cycle (moderate Re-number)
  • time dependent -- a start-up period

how to report the results

To assess the truth the reported data should be

  • independent of numerical setup (like the mesh or the scheme),
  • dimensionless and suitably parametrized (like through the Reynolds number),
  • characteristic for the setup, and
  • meaningful for, say, applications.

Characteristic Outputs

for the stationary case

Variable Definition
\(C_L\) lift coefficient(s)
\(C_D\) drag coefficient(s)
\(C_T\) torque coefficient(s)
\(\Delta_p\) pressure difference at the cylinder
\({\omega}^{ * }\) dimensionless rotation

in the periodic case

We used

  • the Strouhal number to characterize the frequency,
  • minima, maxima of \(C_D\), \(C_L\), \(C_T\), and \(\omega^{ * }\),
  • and \(\Delta_p(t^ * )\) -- at the middle of a period.

Implementation

Code Base

There were 5 independent implementations using established libraries:

Algorithms

  • inf-sup stable and stabilized equal order elements.
  • High-order and standard Taylor-Hood (\(P_2-P_1)\) elements.
  • Divergence conforming elements.
  • Hybrid Discontinous Galerkin methods.
  • Implicit/Explicit time integration.
  • Most critical: Evaluation of the boundary integrals.

Results

The reported (converged) characteristic outputs ly within certain confidence intervals \(\Delta_I\):

Test case Relative size of \(\Delta_I\) Critical value
stationary-2D \(10^{-5}\) \(C_L\)
periodic-2D \(10^{-3}\) \(C_T\)
time-dep-2D \(10^{-3}\) \(C_L\)
stationary-3D (\(1\)), \(10^{-1}\) \(\omega^ { * }\)

Discussion

  • The 2D simulations gave reliable results.
  • Also the stationary 3D case (at least in absolute numbers).
  • The time-dependent 3D results were inconclusive.
  • We did not include them in the report.
  • Conflict with another benchmark property: the numerical setup should be challenging.

Code Availability

Full data sets for the results as well as all implementations can be found at

DOI: 10.5281/zenodo.3253455

Conclusion

Conclusion

  • Benchmarks are valuable for the assessment of numerical models.

  • The proposed benchmark may qualify as such because of
    • reliable data,
    • setup accessible to standard solvers.

  • I learned: Numerical analysis matters.

References

von Wahl, Henry, Thomas Richter, Christoph Lehrenfeld, Jan Heiland, and Piotr Minakowski. 2019. “Numerical Benchmarking of Fluid-Rigid Body Interactions.” Computers & Fluids. doi:10.1016/j.compfluid.2019.104290.