A quadratic decoder approach to nonintrusive reduced-order modeling of nonlinear dynamical systems

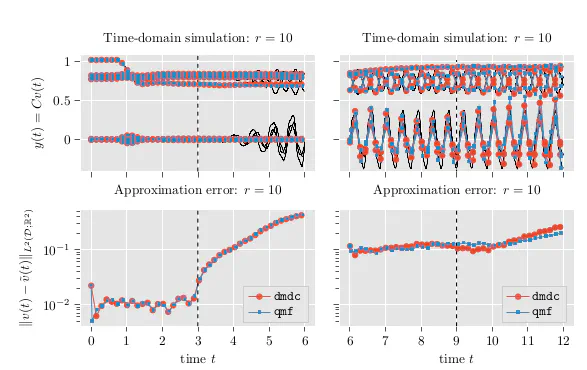
Linear projection schemes like Proper Orthogonal Decomposition can efficiently reduce the dimensions of dynamical systems but are naturally limited, e.g., for convection-dominated problems. Nonlinear approaches have shown to outperform linear methods in terms of dimension reduction versus accuracy but, typically, come with a large computational overhead. In this work, we consider a quadratic reduction scheme which induces nonlinear structures that are well accessible to tensorized linear algebra routines. We discuss that nonintrusive approaches can be used to simultaneously reduce the complexity in the equations and propose an operator inference formulation that respects dynamics on nonlinear manifolds.

4