Ausbreitung von Glitzer und anderen ansteckenden Eigenschaften

Für SchülerUnis bietet sich die Modellierung von Epidemien an, weil die Mechanismen und die Mathematik im Modell nachvollziehbar sind. Bisher hatte mich an meinen Versuchen damit aber gestört, dass

1. das Thema etwas trübe ist (niemand hat Lust auf Corona oder einen Zombie)
2. Es doch abstrakte Mathe bleibt (wenn beispielsweise im deterministischen “SIR”-Modell die Ansteckungsraten einfach angenommen werden)
3. und letztlich die Verbindung zwischen Modell und Person nicht hergestellt wird.

Die Inhalte

Im diesjährigen Versuch zu unserer Sommeruniversität für Schülerinnen habe ich einen neuen Ansatz probiert. Das feedback war positiv und somit teile ich gerne meine Überlegungen und Materialien hier.

Motivation

Mit dem Normalen Kita-Gesetz

Bastelt ein Kind mit Glitzer, dann basteln am Ende alle mit Glitzer

und mit dem Video von Quarks zum Versuch, wie sich im Restaurant die Handcreme einer Frau am Ende überall befindet, wurde unser Experiment motiviert.

Aufbau und Experiment

Dann haben sich die Proband:innen um einen Tisch gesetzt und die Lollipedimie durchgespielt. Das ansteckende Element waren Lollies, die ich verteilt oder eingesammelt habe und der Zufall wurde durch Würfeln eingebracht.

Ein Experiment bestand aus dem Würfeln reihum und der Gliederung

0. Tag – eine Infektionsrunde
1. Tag – zwei Ausbreitungsrunden und eine Genesungsrunde
2. Tag – zwei Ausbreitungsrunden und eine Genesungsrunde
3. Tag – zwei Ausbreitungsrunden und eine Genesungsrunde

mit den Regeln

• bei der Infektionsrunde bekam einen Lollie, wer eine 6️⃣ gewürfelt hat.
• in einer Ausbreitungsrunde bekam einen Lollie, wer eine 5️⃣ oder 6️⃣ warf und wessen Nachbar:in schon einen Lollie hatte
• in einer Genesungsrunde wurde der Lollie abgegeben, falls eine 1️⃣ oder 2️⃣ geworfen wurde

Es wurden 2 Experimente durchgespielt (gesamt etwa 15 Minuten) und die Anzahl der Lollies nach jedem Tag an der Tafel protokolliert. Die Schülerinnen (zwischen 10. und 12. Klasse) hatten es schnell verinnerlicht, shortcuts ausgemacht (wer keine Nachbarin mit Lollie hat, muss gar nicht würfeln) und nach dem zweiten Durchgang wollten manche lieber das Angebot wahrnehmen, die Computersimulation dazu zu sehen.

Mit 11 Schülerinnen ist die Varianz in den Ergebnissen eigentlich recht gross. Aber wie es der Zufall wollte, kamen in unseren Experimenten mehr oder weniger die gleichen Werte raus.

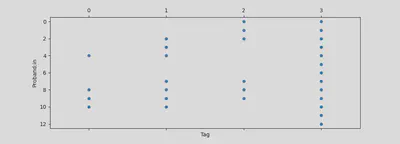
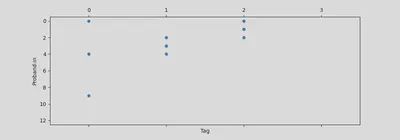
Computersimulation

Die Simulation ermöglicht in der Tat das schnelle Durchspielen der Experimente und illustriert die großen Abweichungen in den Resultaten.

Auch ermöglicht es die Simulation, die Anzahl der Teilnehmer:innen im Stuhlkreis beliebig hoch zu setzen. Die Anwesenden erkannten schnell, dass mit höherer Anzahl, die Prozentzahl der am Ende infizierten, weniger stark schwankte.

Diese Erkenntnis wurde gefestigt in der nachfolgenden Aufgabe, zu der immer zwei Schülerinnen einen Datensatz (mit 50 simulierten Durchläufen) zu jeweils einer Anzahl von Proband:innen bekamen. Diese Daten sollten in ein vorbereitetes Blatt in ein Histogramm (durch ausmalen von Kästchen) überführt wurden. Das und die abschließende Übereinkunft, dass für größere Gruppen, die Bilder weniger wild aussehen, kam wirklich gut an.

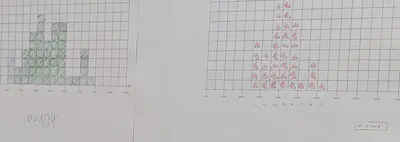
Das reichte dann auch als input, sodass meine abschließende Herleitung von Differentialgleichungen (aus dem Differenzenquotienten der täglichen bzw. stündlichen bzw. minütlichen bzw. … Änderung) zwar nachvollzogen und aufgenommen wurde, aber letztlich nicht nötig gewesen wäre.

Materialien

• genügend Lollies zum Verteilen (vielleicht gehen auch Fähnchen?)
• Würfel und Würfelbecher
• Tafel zur Protokollierung
• Simulationsskript
• Datenblatt (Beispiel), Ausmalhistogramm und geeignete Stifte zum Ausmalen
• alles als zip (auch bspw tikz code zum Anpassen)