10 Automatisches (Algorithmisches) Differenzieren

In der Mathematik und im Bereich der Computeralgebra ist das automatische Differenzieren (auch Auto-Differenzieren, Autodiff oder einfach AD genannt und in anderen communities als algorithmisches Differenzieren oder computergestütztes Differenzieren bezeichnet), ein Satz von Techniken zur Berechnung (der Werte(!)) der partiellen Ableitung einer durch ein Computerprogramm spezifizierten Funktion.

AD nutzt die Tatsache, dass jede Computerberechnung, egal wie kompliziert, eine Sequenz von elementaren arithmetischen Operationen (Addition, Subtraktion, Multiplikation, Division usw.) und elementaren Funktionen (exp, log, sin, cos usw.) ausführt. Durch wiederholte Anwendung der Kettenregel auf diese Operationen können partielle Ableitungen beliebiger Ordnung automatisch, genau bis zur Arbeitspräzision und mit höchstens einem kleinen konstanten Faktor mehr an arithmetischen Operationen als das ursprüngliche Programm berechnet werden.

10.1 Andere Differentiationsmethoden

In manchen Anwendungsfällen wird auf eine symbolische Repräsentation von Funktionen und Variablen in der computergestützten Berechnung zurückgegriffen. Sogenannte Computeralgebra Pakete wie Maple, Mathematica oder die Python Bibliotheken SageMath oder Sympy können dann automatisiert auch Operationen auf Funktionen wie Integralberechnung und eben auch Differentiation exakt ausführen. Durch die Kettenregel und unter der Massgabe, dass alle Codes letztlich nur elementare Funktionen mit bekannten Ableitungen verschalten, wäre es auch möglich, bei entsprechender Implementierung des primären Progamms, auch automatisiert die Ableitungen zu erzeugen. Allerdings ist der Mehraufwand in der symbolischen Programmierung erheblich und die Auswertung der Ausdrücke langsam, sodass symbolische Berechnungen (und entsprechend auch die Möglichkeit der symbolischen automatischen Differentiation) nur in spezifischen und insbesondere nicht in “grossen” und “multi-purpose” Algorithmen zur Anwendung kommen.

Auch AD rechnet symbolisch und rekursiv mit der Kettenregel. Der Unterschied ist, dass AD nur mit Funktionswerten der Ableitungen arbeitet während die symbolische Ableitung versucht, die Ableitung als Funktion zu erzeugen.

Auf der anderen Seite steht die numerische Differentiation (beispielsweise durch Berechnung von Differenzenquotienten). Diese Methode ist universell (Ableitungen können ohne Kenntnis dessen berechnet werden, was im Innern des Programms alles passiert) ist jedoch enorm schlecht konditioniert (da im Zähler des Differenzenquotienten fast gleich grosse Größen subtrahiert werden). Die Bestimmung einer passenden Schrittweite muss immer ad hoc erfolgen und macht diese Berechnung zusätzlich teuer.

Sind höhere Ableitungen gefragt, verstärken sich zudem die Komplexität (für die symbolische Berechnung) und die Fehlerverstärkung (in der numerischen Differentiation).

10.2 Anwendungen

Automatisches Differenzieren ist ein entscheidender Baustein im Erfolg des maschinellen Lernens. Jan könnte sagen, dass ohne AD die Optimierung der neuronalen Netze mit tausenden bis Millionen von Parametern nicht möglich wäre.

10.3 Vorwärts- und Rückwärtsakkumulation

10.3.1 Kettenregel der partiellen Ableitungen zusammengesetzter Funktionen

Grundlegend für die automatische Differentiation ist die Zerlegung von Differentialen, die durch die Kettenregel der partiellen Ableitungen zusammengesetzter Funktionen bereitgestellt wird. Für die einfache Zusammensetzung

\[\begin{align*} y &= f(g(h(x))) = f(g(h(w_0))) = f(g(w_1)) = f(w_2) = w_3 \\ w_0 &= x \\ w_1 &= h(w_0) \\ w_2 &= g(w_1) \\ w_3 &= f(w_2) = y \end{align*}\]

ergibt die Kettenregel für die Werte zu einem fixen Wert \(x^*\) von \(x\):

\[\begin{equation} \begin{split} \frac{\partial y(x^*)}{\partial x} &= \frac{\partial y}{\partial w_2}\Biggl|_{w_2=g(h(x^*))} \frac{\partial w_2}{\partial w_1} \Biggl|_{w_1=h(x^*)}\frac{\partial w_1}{\partial w_0}\Biggl|_{w_0=x^*} \\ &= \frac{\partial f}{\partial w_2}(w_2^*)\biggl[ \frac{\partial g}{\partial w_1}(w_1^*) \Bigl[\frac{\partial h}{\partial x}(w_0^*) \Bigr] \biggr] \end{split} \tag{10.1} \end{equation}\]

Für multivariate Funktionen gilt die mehrdimensionale Kettenregel und das Produkt der Ableitungen wird zum Produkt der Jacobi-Matrizen.

10.4 AD – Vorwärtsmodus

Im sogenannten Vorwärtsmodus (auch forward accumulation) wird jede Teilfunktion im Programm so erweitert, dass mit dem Funktionswert direkt der Wert der Ableitung mitgeliefert wird. Ein Programmfluss für obiges \(f\), \(g\), \(h\) Beispiel würde also jeweils immer zwei Berechnungen machen und die Ableitung akkumulieren:

Schritt	Funktionswert	Ableitung	Akkumulation
0	\(w_0 = x\)	\(\dot w_0 = 1\)	\(1\)
1	\((w_1, \dot w_1) = (h(w_0), h'(w_0))\)	\(\dot w_1\)	\(\dot w_1 \cdot 1\)
2	\((w_2, \dot w_2) = (g(w_1), g(w_1))\)	\(\dot w_2\)	\(\dot w_2 \cdot\dot w_1 \cdot 1\)
3	\((w_3, \dot w_3) = (f(w_1), f(w_1))\)	\(\dot w_3\)	\(\dot w_3 \cdot\dot w_2 \cdot\dot w_1 \cdot 1\)

Das ergibt die Ableitung als den finalen Wert der Akkumulation. Wir bemerken, dass hierbei

• die Ableitung entlang des Programmflusses immer direkt mitbestimmt wird (deshalb vorwärts Modus)
• es genügt im Schritt \(k\), den Wert \(w_{k-1}\) und die Akkumulation zu kennen.
• Für eine Funktion \(F\otimes G \otimes h \colon \mathbb R^{}\to \mathbb R^{m}\), funktioniert die Berechnung ganz analog mit beispielsweise \[\begin{equation*} (G, \partial G) \colon \mathbb R^{} \to \mathbb R^{\ell} \times \mathbb R^{\ell} \end{equation*}\] und \[\begin{equation*} (F, \partial F) \colon \mathbb R^{\ell} \to \mathbb R^{m} \times \mathbb R^{m \times \ell} \end{equation*}\] und der Akkumulation \[\begin{equation*} \frac{\partial y}{\partial x}(x^*) = \partial F(w_2)\cdot \partial G(w_1)\cdot h'(w_0) \cdot 1. \end{equation*}\]
• Für eine Funktion in mehreren Variablen, d.h. von \(\mathbb R^{n}\) nach \(\mathbb R^{m}\), werden die partiellen Ableitungen \(\frac{\partial y}{\partial x_k}\) separat in eigenen Durchläfen berechnet:
  • damit ist an der Implementierung nichts zu ändern, nur die Akkumulation wird mit \(\dot w_0 = \begin{bmatrix} 0 & \dotsm & 1 & 0 & \dotsm & 0 \end{bmatrix}^T\) initialisiert
  • eine simultane Berechnung aller Ableitungen verursacht vergleichsweise viel overhead (entweder müssen die verschiedenen Richtungen im Code organisiert werden oder es müssen alle Zwischenberechnungen der Ableitung gespeichert werden).

Wir halten fest, dass der Vorwärtsmodus gut funktioniert für skalare Eingänge unabhängig von der Zahl der Ausgänge. Wir werden lernen, dass sich beim Rückwärtmodus dieses Verhältnis umdreht. Damit:

• Vorwärtsakkumulation: Bevorzugt für Funktionen \(f \colon \mathbb{R}^n \rightarrow \mathbb{R}^m\), wobei \(n \ll m\).
• Rückwärtsakkumulation: Bevorzugt für Funktionen \(f\colon \mathbb{R}^n \rightarrow \mathbb{R}^m\), wobei \(n \gg m\).

Vor allem für neuronale Netze mit vielen Parametern und dem Fehler als (skalaren) Ausgang, ist der Rückwärtsmodus fraglos die Methode der Wahl. Hier wird dann typischerweise von backpropagation gesprochen, was eine Adaption der Methode an die Architektur typischer neuronaler Netze ist.

Bevor wir zum Rückwärtsmodus kommen, noch einige Praktische Bemerkungen anhand eines konkreten Beispiel.

Zunächst mal die Bemerkung, dass es vorteilhaft ist, ein Programm als ein Graph der die Abhängigkeiten der Variablen enthält, darzustellen. Dann werden insbesondere “nicht vorhandene” Abhängigkeiten vermieden und Speicher– und Rechenaufwand reduziert.

Entsprechend werden die Zwischenwerte \(w_i\) nicht mehr einfach durchnummeriert, sondern es wird von Vorgängern gesprochen

\(w_j\) ist ein Vorgänger von \(w_i\) genau dann wenn \(w_i\) unmittelbar (also explizit) von \(w_j\) abhängt.

Damit (und mit Anwendung der Kettenregel im mehrdimensionalen) wird aus \(\dot w_i = \frac{\partial w_i}{\partial w_{"i-1"}}\) der Ausdruck

\[ \dot w_i = \sum_{j \in \{\text{Vorgänger von i}\}} \frac{\partial w_i}{\partial w_j} \dot w_j \]

Für das Beispiel \[\begin{align*} y &= f(x_1, x_2) \\ &= x_1 x_2 + \sin x_1 \\ &=: w_1 w_2 + \sin w_1 \\ &=: w_3 + w_4 \\ &=: w_5 \end{align*}\] ergibt sich folgender Berechnungsgraph und Fluss in der Vorwärtsakkumulation.

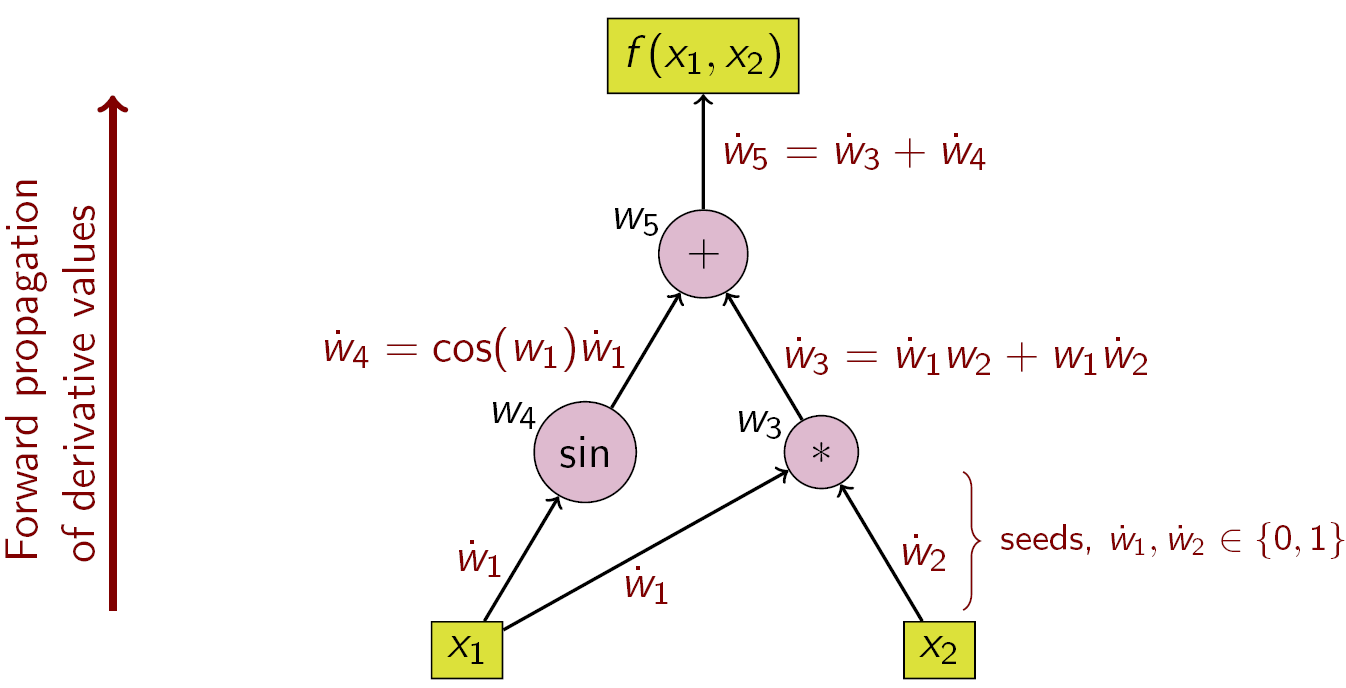
Figure 10.1: Beispiel für Vorwärtsakkumulation mit Berechnungsgraph

Mit den folgenden Schritten ergibt sich für die partielle Ableitung von \(y\) bezüglich \(x_1\)

Schritt	Funktionswert	Ableitung	Akkumulation
0a	\(w_1=x_1\)		\(\dot w_1 = 1\)
0b	\(w_2=x_2\)		\(\dot w_2 = 0\)
1a	\(w_3 = w_1w_2\)	\(\partial w_3 = \begin{bmatrix} w_2&w_1\end{bmatrix}\)	\(\dot w_3 = \begin{bmatrix}w_2&w_1\end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = x_2\)
1b	\(w_4 = \sin(w_1)\)	\(\partial w_4=\cos(w_1)\)	\(\dot w_4 =\cos(w_1)\cdot\dot w_1 = \cos(x_1)\)
2	\(w_5 = w_3 + w_4\)	\(\partial w_5=\begin{bmatrix}1 & 1\end{bmatrix}\)	\(\dot w_5 = \begin{bmatrix}1 & 1\end{bmatrix}\begin{bmatrix} \dot w_3 \\ \dot w_4 \end{bmatrix} = x_2 + \cos(x_1)\)

10.5 Rückwärtsmodus

Bei der Rückwärtsakkumulation werden die sogenannten Adjungierten \[\begin{equation*} \bar{w}_i = \frac{\partial y}{\partial w_i} \end{equation*}\] berechnet. Jan beachte, dass immer \(y\) differenziert wird und dass der gewünschte Ausdruck bei beispielsweise \(\bar x = \frac{\partial y}{\partial x}\) erreicht ist.

Unter Verwendung der Kettenregel ergibt sich die folgende rekursive Formel aus dem Berechnungsgraphen:

\[\bar{w}_i = \sum_{j \in \{\text{Nachfolger von i}\}} \bar{w}_j \frac{\partial w_j}{\partial w_i}\] Sind also spätere Adjungierte \(\bar w_j\) bekannt, können frühere \(\bar w_i\) bestimmt werden.

Die Rückwärtsakkumulation durchläuft die Kettenregel (wie in Gleichung (10.1) von außen nach innen oder im Falle des Berechnungsgraphen (wie in Abbildung 10.2 illustriert) von oben nach unten.

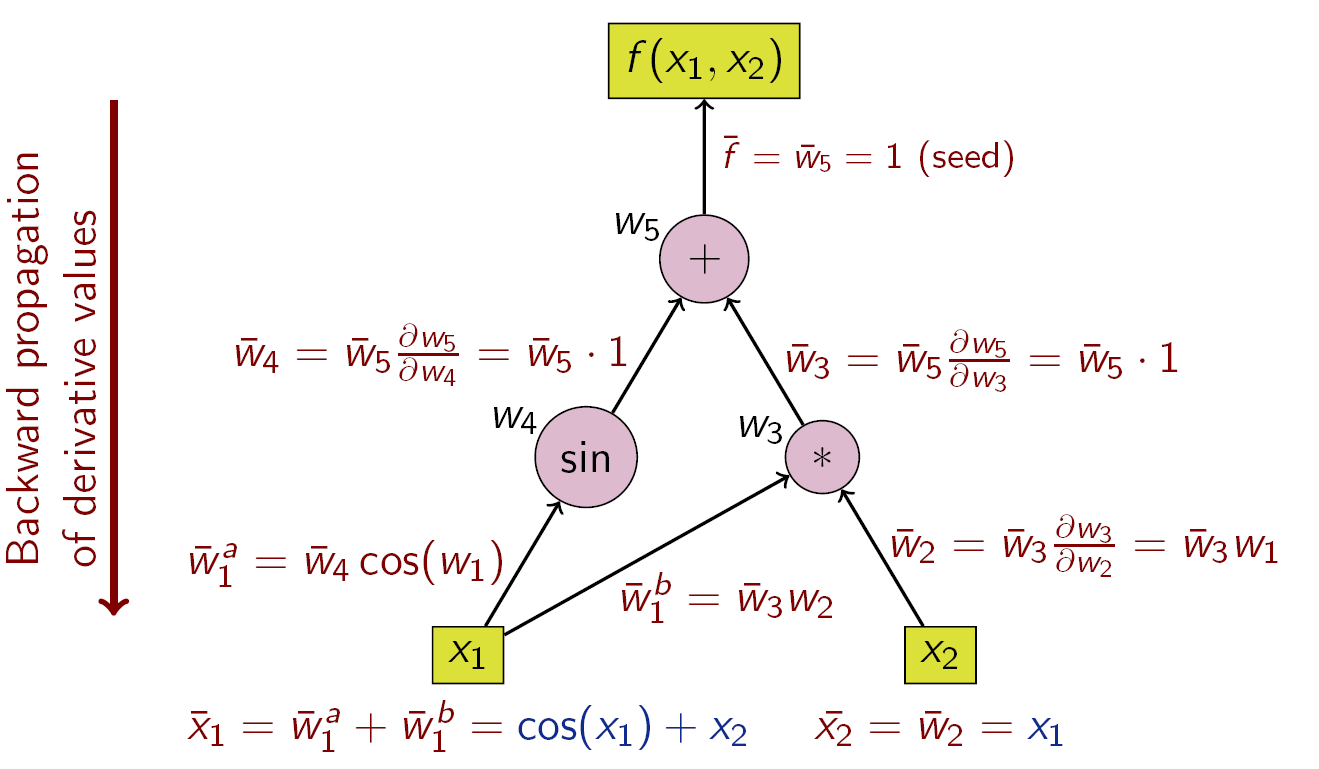
Figure 10.2: Beispiel für Rückwärtsakkumulation mit Berechnungsgraph

Die Operationen zur Berechnung der Ableitung mittels Rückwärtsakkumulation sind in der folgenden Tabelle dargestellt (beachte die umgekehrte Reihenfolge):

Schritt	Funktionswert	Ableitung	Adjungierte
0	\(y=w_5\)	\(\partial y=1\)	\(\bar w_5 = 1\)
1	\(w_5=w_4+w_3\)	\(\partial w_5=\begin{bmatrix} 1&1 \end{bmatrix}\)	\(\bar w_5 = 1\)
2a	\(w_4=\sin(w_1)\)	\(\partial w_4=\cos(w_1)\)	\(\bar w_4 = \bar w_5 \cdot 1 = 1\)
2b	\(w_3=w_1w_2\)	\(\partial w_3=\begin{bmatrix}w_2&w_1\end{bmatrix}\)	\(\bar w_3 = \bar w_5 \cdot 1 = 1\)
3b	\(w_2=x_2\)		\(\bar w_2 = \bar w_3 w_1= x_1\)
3a	\(w_1=x_1\)		\(\bar w_1 = \bar w_3 w_2 +\bar w_4 \cos(w_1) = x_2 + \cos(x_1)\)

Wir bemerken, dass in einem Durchlauf, beide partiellen Ableitungen \[\begin{equation*} \bar w_2 = \frac{\partial y}{\partial w_2}= \frac{\partial y}{\partial x_2},\quad \bar w_1 = \frac{\partial y}{\partial w_1}= \frac{\partial y}{\partial x_1} \end{equation*}\] direkt berechnet werden. Allerdings müssen zunächst in einem Vorwärsdurchlauf die Gradienten \(\partial w_i\) berechnet und gespeichert werden. Das kann bei komplexen Programmen durchaus ein Nachteil sein. Ein Ausweg bietet checkpointing wo nur wenige Zwischenetappen der Werte \(w_i\) gespeichert werden, aus denen bei Bedarf die Nachfolger und Gradienten zwischen den Checkpoints erzeugt werden können.

Zusätzlich muss der Programmablauf (also welche Variablen aus welchen hervorgegangen sind – die sogenannte Wengert Liste) verfügbar sein.

Hätte \(y\) mehrere Komponenten, müsste für jede Komponente die entsprechenden adjungierten in einem neuen Durchlauf berechnet werden.

Andersherum ist es beim Vorwärtsmodus, bei welchem mehrere Komponenten im Ausgang direkt berechnet werden aber für jede Eingangsvariable die Akkumulation separat durchgeführt werden muss.