5 Ein NN Beispiel
Zur Illustration der Konzepte, betrachten wir ein Beispiel in dem ein einfaches Neuronales Netz für die Klassifizierung von Pinguinen anhand vierer Merkmale aufgesetzt, trainiert und auf Funktion geprüft wird.
5.1 Der PENGUINS Datensatz
Die Grundlage ist der Pinguin Datensatz, der eine gern genommene Grundlage für die Illustration in der Datenanalyse ist. Die Daten wurden von Kristen Gorman erhoben und beinhalten 4 verschiedene Merkmale (engl. features) von einer Stichprobe von insgesamt 3441Pinguinen die 3 verschiedenen Spezies zugeordnet werden können oder sollen (Fachbegriff hier: targets). Im Beispiel werden die Klassen mit 0, 1, 2 codiert und beschreiben die Unterarten Adele, Gentoo und Chinstrap der Pinguine. Die Merkmale sind gemessene Länge und Höhe des Schnabels (hier bill), die Länge der Flosse (flipper) sowie das Köpergewicht 2
(body mass).
Wir stellen uns die Frage:
Können wir aus den Merkmalen (features) die Klasse (target) erkennen und wie machen wir gegebenenfalls die Zuordnung?
In höheren Dimensionen ist schon die graphische Darstellung der Daten ein Problem. Wir können aber alle möglichen 2er Kombinationen der Daten in 2D plots visualisieren.
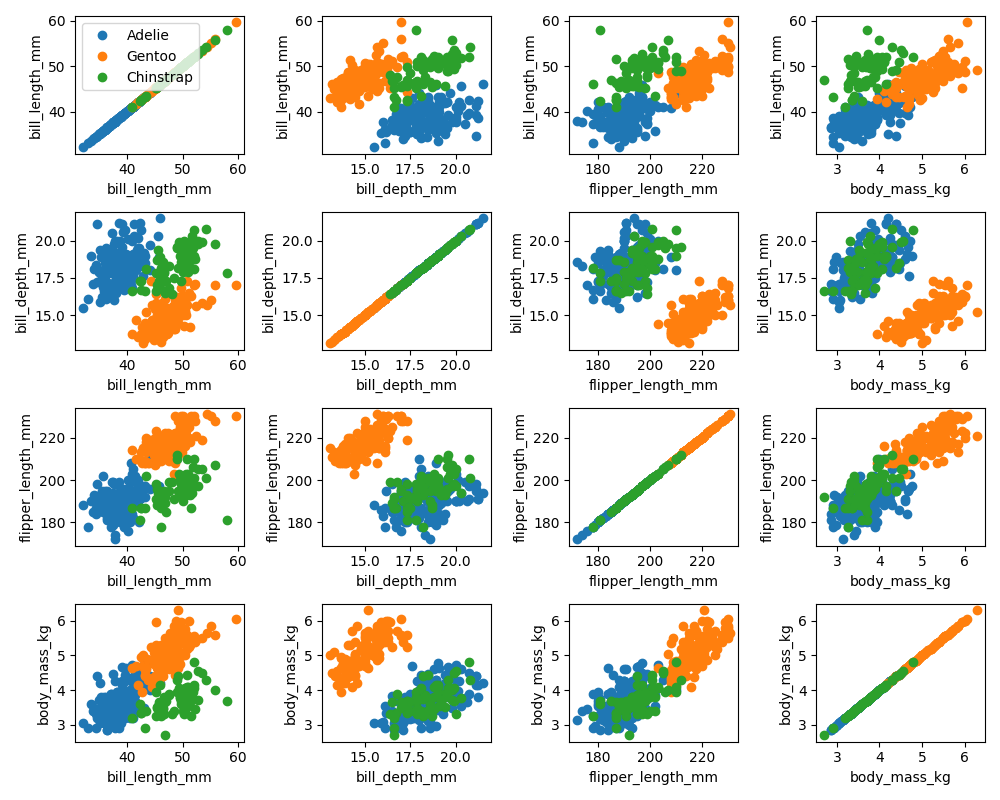
Ein Blick auf die Diagonale zeigt schon, dass manche Merkmale besser geeignet als andere sind, um die Spezies zu unterscheiden. Allerdings reichen (in dieser linearen Darstellung) zwei Merkmale nicht aus, um eine eindeutige Diskriminierung zu erreichen.
5.2 Ein 2-Layer Neuronales Netz zur Klassifizierung
Wir definieren ein neuronales Netzes \(\mathcal N\) mit einer hidden layer als \[\begin{equation*} \eta_i = \mathcal N (x_i):=\tanh \bigl (A_2 \tanh (A_1 x_i + b_1) + b_2\bigr ), \end{equation*}\] das für einen Datenpunkt \(x_i \in \mathbb R^{n_0}\) einen Ergebniswert \(\eta_i\in \mathbb R^{n_2}\) liefert. Die sogenannten Gewichte \(A_1 \in \mathbb R^{n_1 \times n_0}\), \(b_1 \in \mathbb R^{n_1}\), \(A_2 \in \mathbb R^{n_2, n_1}\), \(b_2 \in \mathbb R^{n_2}\) parametrisieren diese Funktion. Eine Schicht besteht aus der einer affin-linearen Abbildung und einer Aktivierungsfunktion die hier als \(\tanh\) gewählt wird und die komponentenweise angewendet wird.
Wir werden \(n_0=4\) (soviele Merkmale als Eingang) und \(n_2=1\) (eine
Entscheidungsvariable als Ausgang) setzen und das Netzwerk so trainieren, dass
anhand der gemessenen Daten \(x_i\) die bekannte Pinguin Population
penguin-data.json in zwei Gruppen aufgeteilt
werden, wobei in der ersten Gruppe eine Spezies enthalten ist und in der anderen
die beiden anderen Spezies.
Dazu kann eine Funktion \(\ell \colon X \mapsto \{-1, 1\}\) definiert werden, die die bekannten Pinguine \(x_i\) aus dem Datensatz \(X\) ihrer Gruppe zuordnet. Dann können die Koeffizienten von \(\mathcal N\) über das Optimierungsproblem \[\begin{equation*} \frac{1}{|X|}\sum_{x_i \in X} \|\ell(x_i)-\mathcal N(x_i)\|^2 \to \min_{A_1, b_1, A_2, b_2} \end{equation*}\] mittels des stochastischen (batch) Gradientenabstiegs bestimmt werden.
Zur Optimierung wird typischerweise ein Teil (z.B. 90%) der Datenpunkte verwendet über die mehrfach (in sogenannten epochs) iteriert wird.
Danach kann mittels der verbliebenen Datenpunkte getestet werden, wie gut das Netzwerk Daten interpretiert, die es noch nicht “gesehen” hat.
5.3 Beispiel Implementierung
Für ein 2-layer Netzwerk zur Klassifizierung der Pinguine.
Hier ein python file oder ein ipython file sowie die Pinguin Daten zum Direktdownload.
5.3.1 Setup
Wir importieren die benötigten Module und laden die Daten.
# import the required modules
import json
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import approx_fprime # we will use this function to compute gradients
# load the data
with open('penguin-data.json', 'r') as f:
datadict = json.load(f)
# turn it into a numpy array
data = np.array(datadict['data'])
data = data - data.mean(axis=0) # center the data
# extract the labels
lbls = np.array(datadict['target'])In diesem Beispiel unterscheiden wir nur zwei Gruppen. Wir teilen die
ersetzen die eigentlichen labels [0, 1, 2] durch die zwei lables [-1, 1].
# a dictionary that maps the labels(=targets) of the data into labels {1, -1}
# that will use for distinction of two groups
mplbldict = {0: np.array([1]),
1: np.array([1]),
2: np.array([-1])}
print('our two groups: \n', [f'{datadict["target_names"][lblid]} --> {mplbldict[lblid].item()}' for lblid in [0, 1, 2]])Als nächstes legen wir die Dimensionen der layers fest und damit auch die Größe der Gewichtsmatrizen. Bei unserem 2-layer Netzwerk, bleibt uns da nur die Größe der mittleren Schicht, da die Eingangsdimension durch die Daten und die Ausgangsdimension durch unsere Wahl, wie wir entscheiden wollen, bereits festgelegt ist.
# sizes of the layers
sxz, sxo, sxt = data.shape[1], 2, mplbldict[0].size
# defines also the sizes of the weightmatricesZuletzt noch die Parameter, die das training definieren.
batchsize– über wieviele Samples wird der stochastische Gradient bestimmtlr– learning rate – die Schrittweiteepochs– wie oft wird über die Daten iteriert
und dann wie gross der Anteil und was die Indizes der Trainings– beziehungsweise Testdaten sind
# parameters for the training -- these worked fine for me
batchsize = 30 # how many samples for the stochastic gradients
lr = 0.125 # learning rate
epochs = 1000 # how many gradient steps
# the data
traindataratio = .9 # the ratio of training data vs. test data
ndata = data.shape[0] # number of datapoints
trnds = int(ndata*traindataratio)
allidx = np.arange(ndata) # indices of all data
trnidx = np.random.choice(allidx, trnds, replace=False) # training ids
tstidx = np.setdiff1d(allidx, trnidx) # test ids5.3.2 Neural Network Evaluation Setup
Hier definieren wir das Netzwerk als Funktion der Parameter und die loss function, die misst wie gut das Netzwerk die Daten wiedergibt und die Grundlage fuer die Optimierung ist.
def fwdnn(xzero, Aone=None, bone=None, Atwo=None, btwo=None):
''' definition/(forward)evaluation of a neural networks of two layers
'''
xone = np.tanh(Aone @ xzero + bone)
xtwo = np.tanh(Atwo @ xone + btwo)
return xtwodef sqrdloss(weightsvector, features=None, labels=None):
''' compute the sqrd `loss`
|| NN(x_i) - y_i ||^2
given the vector of weights for a given data point (features)
and the corresponding label
'''
Aone, bone, Atwo, btwo = wvec_to_wmats(weightsvector)
# compute the prediction
nnpred = fwdnn(features, Aone=Aone, bone=bone, Atwo=Atwo, btwo=btwo)
return np.linalg.norm(nnpred - labels)**2An sich liegen die Parameter als Matrizen vor. Da jedoch die Theorie (und auch die praktische Implementierung) einen Parametervektor voraussetzt, entrollen wir die Matrizen und stecken sie in einen grossen Vektor. Dann muessen wir noch an der richtigen Stelle wieder die Matrizen aus dem Vektor extrahieren; was die folgende Funktion realisiert.
def wvec_to_wmats(wvec):
''' helper to turn the vector of weights into the system matrices
'''
Aone = wvec[:sxz*sxo].reshape((sxo, sxz))
cidx = sxz*sxo
bone = wvec[cidx:cidx+sxo]
cidx = cidx + sxo
Atwo = wvec[cidx:cidx+sxo*sxt].reshape((sxt, sxo))
cidx = cidx + sxo*sxt
btwo = wvec[cidx:]
if Aone.size + bone.size + Atwo.size + btwo.size == wvec.size:
return Aone, bone, Atwo, btwo
else:
raise UserWarning('mismatch weightsvector/matrices')5.3.3 Das Training
Der Parametervektor (“die Gewichte”) werden zufällig initialisiert und dann mit dem stochastischen Gradienten in mehreren Epochen optimiert.
Bemerkung: Hier benutzen wir scipy.optimize.approx_fprime um den
Gradienten numerisch zu bestimmen. Das ist hochgradig ineffizient. “Richtige”
Implementierungen von Machine Learning Bibliotheken benutzen anstelle
Automatisches Differenzieren für eine sowohl schnelle und als auch akkurate Berechnung des Gradienten.
# initialization of the weights
wini = np.random.randn(sxo*sxz + sxo + sxt*sxo + sxt)
gradnrml = [] # list of norm of grads for plotting later
cwghts = wini # the current state of the weight vector
for kkk in range(epochs):
cids = np.random.choice(trnidx, batchsize, replace=False)
cgrad = np.zeros(wini.shape)
for cid in cids:
itrgts = data[cid, :]
ilabls = mplbldict[lbls[cid]]
cgrad = cgrad + approx_fprime(cwghts, sqrdloss, 1e-8,
itrgts, ilabls)
cwghts = cwghts - lr*1/batchsize*cgrad # the upgrade
gradnrml.append(1/batchsize*np.linalg.norm(cgrad))
if np.mod(kkk, 50) == 0:
print(f'k={kkk}: norm of gradient: {np.linalg.norm(cgrad)}')plt.figure()
plt.semilogy(gradnrml, label='norm of gradient estimate')
plt.xlabel('$k$-th stochastic gradient step')
plt.legend()
plt.show()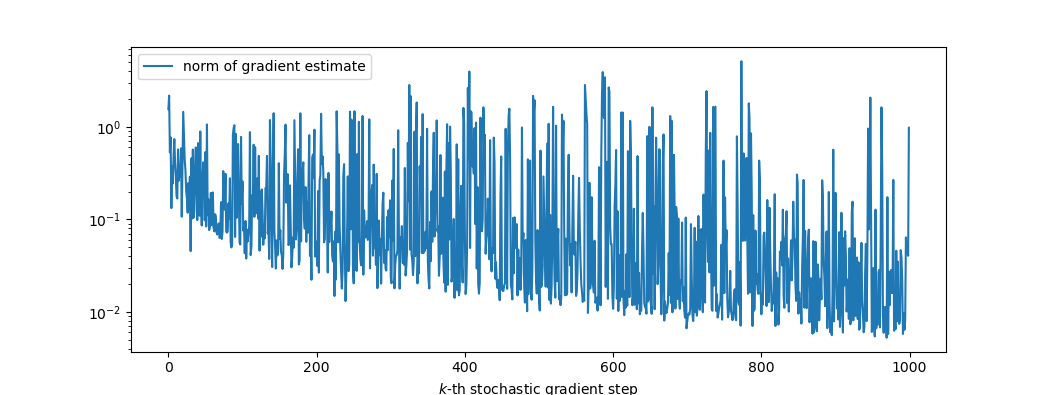
Wir koennen eine gewisse Konvergenz beobachten (sichtbar an der unteren Kante) aber auch ein typisches stochastisches Verhalten.
5.3.4 Das Auswerten
Wir nehmen das Ergebnis der letzten Iteration als beste Parameter, definieren damit das Neuronale Netz, und testen auf den übriggebliebenen Daten das Ergebnis.
print('***** testing the classification *****')
faillst = []
for cti in tstidx: # iteration over the test data points
itrgt = data[cti, :]
ilbl = mplbldict[lbls[cti]]
# the prediction of the neural network
nnlbl = fwdnn(itrgt, Aone=Aonex, bone=bonex, Atwo=Atwox, btwo=btwox)
sccs = np.sign(ilbl) == np.sign(nnlbl)
print(f'label: {ilbl.item()} -- nn: {nnlbl.item():.4f} -- success: {sccs}')
if not sccs:
faillst.append((cti, ilbl.item(), nnlbl.item(),
datadict['target_names'][lbls[cti]]))
else:
passprint('\n***** Results *****')
print(f'{100-len(faillst)/tstidx.size*100:.0f}% was classified correctly')
print('***** Misses *****')
if len(faillst) == 0:
print('None')
else:
for cfl in faillst:
cid, lbl, nnlbl, name = cfl
print(f'ID: {cid} ({name} pinguin) was missclassified ' +
f'with score {nnlbl:.4f} vs. {lbl}')