7 PCA und weitere SVD Anwendungen

7.1 Proper-Orthogonal Decomposition – POD

Die POD Methode ist ein Ansatz um den hohen Rechen– und Speicheraufwand in der Simulation von hochdimensionalen (d.h. viele Variable umfassenden) Simulationen von dynamischen Systemen abzumildern. Grob gesagt funktioniert POD wie folgt.

Es sei ein dynamisches System \[\begin{equation*} \dot y(t) = f(t, y(t)), \quad y(0)=y_0 \in \mathbb R^{m} \end{equation*}\] gegeben, das die Entwicklung eines Zustandes \(y(t)\in \mathbb R^{m}\) über die Zeit \(t>0\) beschreibt. Je größer die Dimension \(m\) ist, desto aufwändiger ist das numerische berechnen (bzw. approximieren) der Werte von \(y\).

Die Idee von POD ist

1. anzunehmen, dass die Zustände \(y(t)\) mit weniger als \(m\) Koordinaten beschrieben werden können, also \[\begin{equation*} y(t) \approx V\hat y(t) \end{equation*}\] mit einer Basismatrix \(U_r\in \mathbb R^{m\times r}\), \(r\leq m\), und reduzierten Koordinaten \(\hat y(t)\in \mathbb R^{r}\)

2. die Matrix \(U_r\) aus der Rang-\(r\)-Bestapproximation⁷ der Datenmatrix \[\begin{equation*} Y = \begin{bmatrix} y(t_1) & y(t_2) & \hdots & y(t_k) \end{bmatrix}, \end{equation*}\] als die Matrix der ersten \(r\) Singulärvektoren zu bestimmen.

3. und dann das System auf den Spann von \(U_r\) (also auf \(r\) Dimensionen) zu projizieren.

7.2 Simultane Diagonalisierung

Sind zwei symmetrische positiv definite Matrizen \(P \in \mathbb R^{n\times n}\) und \(Q\in \mathbb R^{n\times n}\) gegeben, so gibt es immer eine invertierbare Matrix \(T\in \mathbb R^{n\times n}\), sodass die transformierten Matrizen \[\begin{equation*} \tilde P := TPT^*=: D, \quad \tilde Q := T^{-*}QT^{-1} = D \end{equation*}\] identisch und diagonal sind. Eine Möglichkeit, die Existenz von \(T\) zu beweisen (und auch eine numerisch zu berechnen) funktioniert über die SVD (vgl. die bald erscheinende Übungsaufgabe).

7.3 PCA

Principal Component Analysis ist ein Ansatz aus der Statistik, multivariate Daten so zu transformieren, dass

• die einzelnen Komponenten (empirisch)⁸ nicht mehr korreliert sind
• die Varianz sich hierarchisch absteigend in den ersten Komponenten konzentriert.

Weil ich den Ansatz gerne ad hoc also am Problem entlang motivieren und einführen will, vorweg schon mal die bevorstehenden Schritte

1. Zentrierung/Skalierung der Daten.
2. Berechnung der Varianzen im Standard Koordinatensystem.
3. Überlegung, dass Daten in einem anderen Koordinatensystem eventuell besser dargestellt werden.
4. Berechnung eines optimalen Koordinatenvektors mittels SVD.

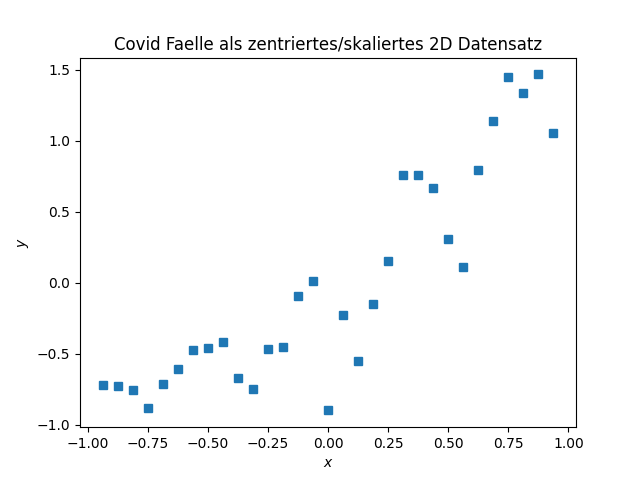
Wir nehmen noch einmal die Covid-Daten her, vergessen kurz, dass es sich um eine Zeitreihe handelt und betrachten sie als Datenpunkte \((x_i, y_i)\), \(i=1,\dotsc,N\), im zweidimensionalen Raum mit Koordinaten \(x\) und \(y\).

Als erstes werden die Daten zentriert indem in jeder Komponente der Mittelwert \[\begin{equation*} x_c = \frac 1N \sum_{i=1}^N x_i, \quad y_c = \frac 1N \sum_{i=1}^N y_i. \end{equation*}\] abgezogen wird und dann noch mit dem inversen des Mittelwerts skaliert.

Also, die Daten werden durch \((\frac{x_i-\bar x}{\bar x},\, \frac{y_i-\bar y}{\bar y})\) ersetzt.

Fallzahlen von Sars-CoV-2 in Bayern im Oktober 2020 – zentriert

7.3.1 Variationskoeffizienten

Als nächstes kann Jan sich fragen, wie gut die Daten durch ihren Mittelwert beschrieben werden und die Varianzen berechnen, die für zentrierte Daten so aussehen

\[\begin{equation*} s_x^2 = \frac {1}{N-1} \sum_{i=1}^N x_i^2, \quad s_y^2 = \frac {1}{N-1} \sum_{i=1}^N y_i^2. \end{equation*}\]

Im gegebenen Fall bekommen wir \[\begin{equation*} s_x^2 \approx 0.32 \quad s_y^2 \approx 0.57 \end{equation*}\] und schließen daraus, dass in \(y\) Richtung viel passiert und in \(x\) Richtung nicht ganz so viel. Das ist jeder Hinsicht nicht befriedigend, wir können weder

• Redundanzen ausmachen (eine Dimension der Daten vielleicht weniger wichtig?) noch
• dominierende Richtungen feststellen (obwohl dem Bild nach so eine offenbar existiert)

und müssen konstatieren, dass die Repräsentation der Daten im \((x,y)\) Koordinatensystem nicht optimal ist.

Die Frage ist also, ob es ein Koordinatensystem gibt, dass die Daten besser darstellt.

Ein Koordinatensystem ist nichts anderes als eine Basis. Und die Koordinaten eines Datenpunktes sind die Komponenten des entsprechenden Vektors in dieser Basis. Typischerweise sind Koordinatensysteme orthogonal (das heißt eine Orthogonalbasis) und häufig noch orientiert (die Basisvektoren haben eine bestimmte Reihenfolge und eine bestimmte Richtung).

7.3.2 Koordinatenwechsel

Sei nun also \(\{b_1,b_2\}\subset \mathbb R^{2}\) eine orthogonale Basis.

Wie allgemein gebräuchlich, sagen wir orthogonal, meinen aber orthonormal. In jedem Falle soll gelten \[\begin{equation*} b_1^T b_1=1, \quad b_2^Tb_2=1, \quad b_1^Tb_2 = b_2^Tb_1 = 0. \end{equation*}\]

Wir können also alle Datenpunkte \(\mathbf x_i = \begin{bmatrix} x_i \\ y_i \end{bmatrix}\) in der neuen Basis darstellen mit eindeutig bestimmten Koeffizienten \(\alpha_{i1}\) und \(\alpha_{i2}\) mittels \[\begin{equation*} \mathbf x_i = \alpha_{i1}b_1 + \alpha_{i2}b_2. \end{equation*}\] Für orthogonale Basen sind die Koeffizienten durch testen mit dem Basisvektor einfach zu berechnen: \[\begin{align*} b_1^T\mathbf x_i = b_1^T(\alpha_{i1}b_1 + \alpha_{i2}b_2) = \alpha_{i1}b_1^Tb_1 + \alpha_{i2}b_1^Tb_2 = \alpha_{i1}\cdot 1 + \alpha_{i2} \cdot 0 = \alpha_{i1},\\ b_2^T\mathbf x_i = b_2^T(\alpha_{i1}b_1 + \alpha_{i2}b_2) = \alpha_{i1}b_1^Tb_2 + \alpha_{i2}b_2^Tb_2 = \alpha_{i1}\cdot 0 + \alpha_{i2}\cdot 1 = \alpha_{i2}. \end{align*}\] Es gilt also \[\begin{equation*} \alpha_{i1} = b_1^T\mathbf x = b_1^T\begin{bmatrix} x_i \\ y_i \end{bmatrix}, \quad \alpha_{i2} = b_2^T\mathbf x_i = b_2^T\begin{bmatrix} x_i \\ y_i \end{bmatrix}. \end{equation*}\]

Damit, können wir jeden Datenpunkt \(\mathbf x_i=(x_i, y_i)\) in den neuen Koordinaten \((\alpha_{i1}, \alpha_{i2})\) ausdrücken.

Zunächst halten wir fest, dass auch in den neuen Koordinaten die Daten zentriert sind. Es gilt nämlich, dass \[\begin{align*} \frac 1N \sum_{i=1}^N \alpha_{ji}=\frac 1N \sum_{i=1}^N b_j^T\mathbf x_i =\frac 1N b_j^T \sum_{i=1}^N \begin{bmatrix} x_i \\ y_i \end{bmatrix} =& \frac 1N b_j^T \begin{bmatrix} \sum_{i=1}^N x_i \\ \sum_{i=1}^N y_i \end{bmatrix}\\ &=b_j^T \begin{bmatrix} \frac 1N \sum_{i=1}^N x_i \\ \frac 1N \sum_{i=1}^N y_i \end{bmatrix} =b_j^T \begin{bmatrix} 0 \\ 0 \end{bmatrix} = 0, \end{align*}\] für \(j=1,2\).

Desweiteren gilt wegen der Orthogonalität von \(B=[b_1~b_2]\in \mathbb R^{2\times 2}\), dass \[\begin{equation*} x_{i}^2 + y_{i}^2 = \|\mathbf x_i\|^2 = \|B^T\mathbf x_i\|^2 = \|\begin{bmatrix} b_1^T \\ b_2^T \end{bmatrix} \mathbf x_i\|^2 = \|\begin{bmatrix} b_1^T\mathbf x \\ b_2^T\mathbf x \end{bmatrix}\|^2 = \|\begin{bmatrix} \alpha_{i1} \\ \alpha_{i2} \end{bmatrix}\|^2 = \alpha_{i1}^2 + \alpha_{i2}^2 \end{equation*}\] woraus wir folgern, dass in jedem orthogonalen Koordinatensystem, die Summe der beiden Varianzen die gleiche ist: \[\begin{equation*} s_x^2 + s_y^2 = \frac{1}{N-1}\sum_{i=1}^N(x_i^2 + y_i^2) = \frac{1}{N-1}\sum_{i=1}^N(\alpha_{i1}^2 + \alpha_{i2}^2) =: s_1^2 + s_2^2. \end{equation*}\]

Das bedeutet, dass durch die Wahl des Koordinatensystems die Varianz als Summe nicht verändert wird. Allerdings können wir das System so wählen, dass eine der Varianzen in Achsenrichtung maximal wird (und die übrige(n) entsprechend klein).

Analog gilt für den eigentlichen Mittelwert der (nichtzentrierten) Daten, dass die Norm gleich bleibt. In der Tat, für die neuen Koordinaten des Mittelwerts gilt in der Norm \[\begin{equation*} \| \begin{bmatrix} \alpha_{c1} \\ \alpha_{c2} \end{bmatrix} \| = \| B^T \begin{bmatrix} x_c \\ y_c \end{bmatrix} \| = \| \begin{bmatrix} x_c \\ y_c \end{bmatrix} \|. \end{equation*}\]

7.3.3 Maximierung der Varianz in (Haupt)-Achsenrichtung

Wir wollen nun also \(b_1\in \mathbb R^{2}\), mit \(\|b_1\|=1\) so wählen, dass \[\begin{equation*} s_1^2 = \frac{1}{N-1}\sum_{i=1}^n \alpha_{i1}^2 \end{equation*}\] maximal wird. Mit der Matrix \(\mathbf X\) aller Daten \[\begin{equation*} \mathbf X = \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ \vdots & \vdots \\ x_N & y_N \end{bmatrix} = \begin{bmatrix} \mathbf x_1^T\\ \mathbf x_2^T \\ \vdots \\ \mathbf x_N^T \end{bmatrix} \in \mathbb R^{N\times 2} \end{equation*}\] können wir die Varianz in \(b_1\)-Richtung kompakt schreiben als \[\begin{equation*} s_1^2 = \frac{1}{N-1}\sum_{i=1}^n \alpha_{i1}^2 = \frac{1}{N-1}\sum_{i=1}^n (b_1^T\mathbf x_i)^2 = \frac{1}{N-1}\sum_{i=1}^n (\mathbf x_i^Tb_1)^2 = \frac{1}{N-1}\| \mathbf X b_1 \|^2 \end{equation*}\] Wir sind also ein weiteres mal bei einem Optimierungsproblem (diesmal mit Nebenbedingung) angelangt:

Lemma 7.1 (Maximale Varianz) Die Lösung des Varianz-Maximierungsproblem (7.1) ist mit \(b=v_1\) gegeben, wobei \(v_1\) der erste (rechte) Singulärvektor von \(\mathbf X\) ist: \[\begin{equation*} \mathbf X = U \Sigma V^T = U \Sigma \begin{bmatrix} v_1^T \\ v_2^T \end{bmatrix}. \end{equation*}\]

Proof. Ein etwas indirekter Beweis basiert auf der Feststellung dass in (7.1) genau die 2-Norm der Matrix \(X\) gesucht ist und dass bei \(v_1\) das Maximum realisiert wird.

Damit rechnen wir auch direkt nach, dass im neuen Koordinatensystem \(\{b_1, b_2\}=\{v_1, v_2\}\) die Varianzen \(s_1^2\) und \(s_2^2\) (bis auf einen Faktor von \(\frac{1}{N-1}\)) genau die quadrierten Singulärwerte von \(\mathbf X\) sind: \[\begin{align*} (N-1)s_1^2 = \|\mathbf X v_1 \|^2 = \|U \Sigma \begin{bmatrix} v_1^T \\ v_2^T \end{bmatrix}v_1\|^2 = \|\Sigma \begin{bmatrix} v_1^Tv_1 \\ v_2^T v_1\end{bmatrix}\|^2 = \|\Sigma \begin{bmatrix} 1 \\ 0\end{bmatrix}\|^2 =\sigma_1^2,\\ (N-1)s_2^2 = \|\mathbf X v_2 \|^2 = \|U \Sigma \begin{bmatrix} v_1^T \\ v_2^T \end{bmatrix}v_2\|^2 = \|\Sigma \begin{bmatrix} v_1^Tv_2 \\ v_2^T v_2\end{bmatrix}\|^2 = \|\Sigma \begin{bmatrix} 0 \\ 1\end{bmatrix}\|^2 =\sigma_2^2 \end{align*}\]

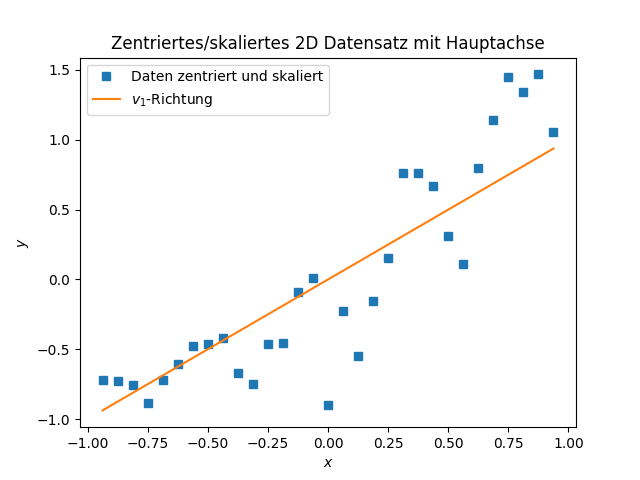
Für unser Covid Beispiel ergibt sich \[\begin{equation*} V^T \approx \begin{bmatrix} 0.5848 & 0.8111 \\ 0.8111 & -0.5848 \end{bmatrix} \end{equation*}\] also \[\begin{equation*} b_1 = v_1 = \begin{bmatrix} 0.5848 \\ 0.8111 \end{bmatrix} \quad b_2 = v_2 = \begin{bmatrix} 0.8111 \\ -0.5848 \end{bmatrix} \end{equation*}\] als neue Koordinatenrichtungen mit \[\begin{equation*} s_1^2 \approx 0.85, \quad s_2^2 \approx 0.04, \end{equation*}\] was bereits eine deutliche Dominanz der \(v_1\)-Richtung – genannt Hauptachse – zeigt.

Im Hinblick auf Anwendungen und Eigenschaften der PCA untersuchen werden, noch ein Plot der Daten mit der \(v_1\)-Richtung als Linie eingezeichnet.

Fallzahlen von Sars-CoV-2 in Bayern im Oktober 2020 – zentriert/skaliert/Hauptachse