8 Support Vector Machines
In diesem Kapitel betrachten wir, wie das Klassifizierungsproblem (erstmal bezüglich zweier Merkmale) durch eine optimale Wahl einer trennenden Hyperebene gelöst werden kann. In der Tat sind die Merkmale der SVM
- dass die beste Hyperebene
- effizient berechnet wird
- und das sogar für möglicherweise nichtlineare Einbettungen in höhere Dimensionen (kernel-SVM)
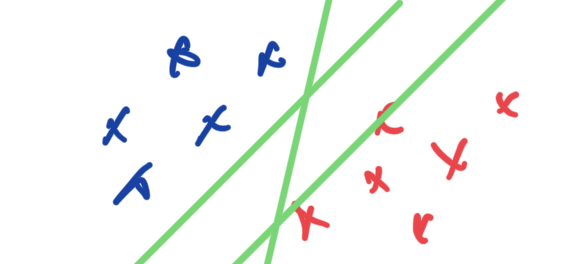
8.1 Problemstellung
Definition 8.1 (Problemstellung für die SVM)
Gegeben sei eine Wolke im \(\mathbb R^{n}\) von \(N\) Datenpunkten \[\mathbb X := \bigl \{(x_i,y_i)\colon x_i \in \mathbb R^{n}, \, y_i\in \{-1,+1\}, \, i=1,\dotsc, N\bigr \}\] wobei \(x_i\) der Datenpunkt ist und \(y_i\) das zugehörige Label.
Eine Hyperebene \(H\subset \mathbb R^{n}\), definiert durch den Stützvektor \(b\subset \mathbb R^{n}\) und den Normalenvektor \(w\in \mathbb R^{n}\), heißt trennend, falls \(H\) heißt Support Vector Machine falls, \(H\) die Hyperebene ist, für die der kleinste Abstand \[d(H, \mathbb X) = \min_{s\in H, i=1, \dotsc, N}\{\|s-x_i\|_2\}\] maximal wird.
Ein Paar Bemerkungen dazu.
- Dass die Labels mit \(\pm 1\) gewählt werden hat ganz praktische Gründe:
- Zunächst lässt sich anhand des Vorzeichen des inneren Produktes \(\bigl \langle x-b, \, w\bigr\rangle \) entscheiden, auf welcher Seite von \(H\) ein Punkt \(x\) liegt. (Punkte auf der gleichen Seite haben das gleiche Vorzeichen). Mit der Wahl der labels als \(\pm 1\) kann das kompakt in einer einzigen Gleichung wie in (8.1) in der Definition geschrieben werden.
- Ist die Hyperebene bekannt, können neue Datenpunkte \(x\) über das Vorzeichen von \(\bigl \langle x-b, \, w\bigr\rangle \) gelabelt werden – das ist die eigentliche Motivation, diese Hyperebene möglichst gut zu bestimmen.
- Es gilt \(\bigl \langle x-b, \, w\bigr\rangle =\bigl \langle x, \, w\bigr\rangle -\bigl \langle b, \, w\bigr\rangle :=\bigl \langle x, \, w\bigr\rangle -\beta\). Und damit genügt es zur Definition (und zum Einsatz in der Klassifizierung), nur den Vektor \(w\in \mathbb R^{n}\) und den bias \(\beta \in \mathbb R^{}\) zu bestimmen (beziehungsweise zu kennen).
- Klassischere Methoden zur Klassifizierung mittels Hyperebene benutzen beispielsweise einfache neuronale Netze um ein passendes \((w, \beta)\) zu bestimmen.
- Eine solche Hyperebene kann durchaus auch nicht existieren, dann heißen die Daten nicht linear trennbar. Existiert eine solche Ebene, dann existieren unendlich viele – ein weiterer Grund, die Ebene optimal (und damit hoffentlich eindeutig) zu wählen.
8.2 Maximierung des Minimalen Abstands
Um den Abstand maximieren zu können leiten wir eine Formel her.
Dazu sei \(w\in \mathbb R^{n}\) der Normalenvektor von \(H\) sei \(h\in \mathbb R^{}\) so, dass \(b=\frac{h}{\|w\|}w\) ein Stützvektor ist. (Insbesondere kann Jan eine Hyperebene auch über den Normalenvektor und den Abstand von \(H\) zum Ursprung charakterisieren). Damit bekommen wir den Abstand von \(H\) zum Ursprung als \(h\) (Achtung: das \(h\) kann auch negativ sein – es sagt uns wie weit müssen wir den normalisierten Vektor \(w\) entlanglaufen, bis wir zu Ebene \(H\) gelangen).
Zu einem beliebigen Punkt \(x\in \mathbb R^{n}\) bekommen wir den Abstand zu \(H\) als
- den Abstand der Ebene \(H\) zur Ebene \(H_x\), die parallel zu \(H\) verläuft und \(x\) enthält
- beziehungsweise als die Differenz der Abstände von \(H_x\) und \(H\) zum Ursprung
Da auch \(w\) der Normalenvektor von \(H_x\) ist, gilt für den Abstand \(h'\), dass \[\begin{equation*} h_x = \|x\|_2\cos(\phi(w,x))=\|x\|_2 \frac{\bigl \langle w, \, x\bigr\rangle }{\|w\|_2\|x\|_2} = \frac{\bigl \langle w, \, x\bigr\rangle }{\|w\|_2} \end{equation*}\] wobei \(\cos(\phi(w, x))\) aus dem Winkel zwischen \(x\) und \(w\) herrührt.
Mit dieser Formel und mit \(b=hw\), erkennen wir, dass der Test auf das Vorzeichen \[\begin{equation*} \bigl \langle x-b, \, w\bigr\rangle = \bigl \langle x-\frac{h}{\|w\|_2} w, \, w\bigr\rangle = \bigl \langle x, \, w\bigr\rangle - h\|w\|_2 = \|w\|_2 (\frac{\bigl \langle x, \, w\bigr\rangle }{\|w\|_2} - h) = \|w\|_2(h_x - h) \end{equation*}\] den mit \(\|w\|_2\) skalierten Abstand (inklusive dem Vorzeichen) enthält, beziehungsweise, dass der Abstand als \[\begin{equation*} y_i\frac{\bigl \langle x_i-b, \, w\bigr\rangle }{\|w\|_2} = y_i\frac{\bigl \langle x_i, \, w\bigr\rangle -\beta}{\|w\|_2} \end{equation*}\] (für eine trennende Hyperebene \((w, \beta)\)) auch immer das richtige Vorzeichen erhält (da \(\|w\|_2>0\). Dementsprechend kann das SVM Problem als \[\begin{equation*} \max_{w\in \mathbb R^{n}, \, \beta \in \mathbb R^{}} \min_{x_i \in \mathbb X} y_i\frac{\bigl \langle x_i, \, w\bigr\rangle -\beta}{\|w\|_2} \end{equation*}\] formuliert werden.
So ein \(\min \max\) Problem ist generell schwierig zu analysieren und zu berechnen. Aber wir können direkt sagen, dass die Zulässigkeit der Optimierung gesichert ist, da “der \(\max\)-imierer” nach Möglichkeit eine trennende Hyperebene wählt und so schon mal sicherstellt, dass “der \(\min\)-inimierer” nur über positive Zahlen minimiert.
Darüberhinaus, wenn eine trennendes Hyperebene existiert, sodass \[\begin{equation*} y_i(\bigl \langle x_i, \, w\bigr\rangle -\beta) = y_i(\bigl \langle x_i, \, w\bigr\rangle -h \|w\|_2) \geq q > 0 \end{equation*}\] dann können wir durch die Wahl von \(\tilde w =\frac 1q w\), immer erreichen, dass das Minimum \(\min_{ x_i \in \mathbb X} y_i \bigl \langle x_i, \, w\bigr\rangle -\beta=1\) ist und das Max-Min durch ein Maximierungsproblem unter Zulässigkeitsnebenbedingungen \[\begin{equation*} \min_{w,\beta} \frac 12 \|w\|_2^2, \quad{s.t.}\quad y_i(\bigl \langle x_i, \, w\bigr\rangle -\beta) \geq 0, \, i=1,\dotsc, N \end{equation*}\] ersetzen. Dabei haben wir noch ausgenutzt, dass \(\max_w \frac 1{\|w\|}\leftrightarrow \min_w \frac 12 \|w\|^2\) entspricht, um die Standardform eines quadratischen Optimierungsproblems unter (affin) linearen Ungleichungsnebenbedingungen zu erhalten.
Für solche Optimierungsprobleme kann das duale Problem direkt hergeleitet werden, was sich in diesem Fall als die Suche eines Vektors \(a\in \mathbb R^{n}\) über das restringierte Minimierungsproblem \[\begin{equation*} \min_{a} \left(\frac 12 \sum_{i=1}^N\sum_{k=1}^Na_ia_k y_i y_k \bigl \langle x_i, \, x_k\bigr\rangle - \sum_{i=1}^N a_i\right) \quad{s.t.}\quad a\geq0, \, \sum_{i=1}^Na_iy_i=0 \end{equation*}\] ergibt.
Aus der KKT Theorie kann abgeleitet werden, dass \(a_i>0\), genau dann wenn \(x_i\) die Gleichheit \(y_i(\bigl \langle x_i, \, w\bigr\rangle -\beta)=1\) erfüllt ist, also \(x_i\) ein sogenannter support vector ist. Ist \(S\) die Menge aller Indices, die die support vectors indizieren, so kann die Klassifikation eines neuen Datenpunktes \(x\) mittels \[\begin{equation*} y(x) = \sum_{i\in S}a_iy_i\bigl \langle x, \, x_i\bigr\rangle +\gamma \end{equation*}\] vorgenommen werden, wobei der bias als \[\begin{equation*} \gamma = \sum_{i\in S}(y_i - \sum_{k\in S}a_ky_k\bigl \langle x_i, \, x_k\bigr\rangle ) \end{equation*}\] vorberechnet werden kann.
8.2.1 Nichtlineare Separation
Existiert auf den Originaldaten keine separierende Hyperebene (oder ist sie schwer zu berechnen) dann können die Daten in höhere Dimensionen nichtlinear eingebettet werden und dort separiert werden.
\[\begin{equation*} \Psi \colon \mathbb R^{n} \to \mathbb R^{M} \end{equation*}\]
Beispiel von gestern \[\begin{equation*} \Psi\colon \mathbb R^{} \to \mathbb R^{2}\colon x \to \Psi(x) = (x, (x-2)^2) \end{equation*}\]
Mit der erhöhten Dimension kommen zwei Aufgaben mit einer Lösung
Die transformierten Daten müssen separiert und neue Daten müssen klassifiziert werden – das ist schwierig und aufwändig für \(N\gg 1\).
Wie soll \(\Psi\) gewählt werden?
Die Lösung zu beidem ist, dass
- in der dualen Formulierung nur Skalarprodukte \(\bigl \langle x_i, \, x_j\bigr\rangle \) beziehungsweise \(\bigl \langle \Psi(x_i), \, \Psi(x_j)\bigr\rangle \) benötigt werden
- die bestenfalls durch kernel Funktionen einfach berechnet werden können (ohne das Lifting in den hochdimensionalen Raum)
Beispiele:
- \(\Psi(x_1, x_2) = (x_1^2, \sqrt{2}x_1x_2, x_2^2)\) hat die kernel Funktion \(k(x,y)=(x_1y_1+x_2y_2)^2\)
Damit wird zunächst das Berechnungsproblem gelöst. Das Problem, welche Funktionen gewählt werden, wird nebenbei dadurch gelindert, dass
- die Effizienz in der Auswertung try and error möglich macht
- Jan letztlich gar keine \(\Psi\)s mehr sucht, sondern nur noch \(k\)s mit bekannten Eigenschaften.