9 Best and Universal Approximation

Alle bisher betrachteten Approximationsprobleme waren in Bezug auf eine 2-norm (“least squares”) formuliert. Die für die Berechnung unmittelbaren Vorteile sind die

  1. Differenzierbarkeit der Norm und die
  2. Charakterisierung der Optimallösung über Orthogonalität.

Ein gängiges Optimierungsproblem, eine Bestapproximation zu einer stetigen Funktion \(f\colon [a, b]\to \mathbb R^{}\) in einer passenden Menge von Funktionen \(\mathcal G\) bezüglich der Supremumsnorm9 zu finden \[\begin{equation*} \min_{g\in \mathcal G} \|f-g\|_\infty = \min_{g \in \mathcal G}\bigl (\max_{x\in [a, b]}|f(x)-g(x)|\bigr ) \end{equation*}\] fällt nicht darunter. Die entstehenden Schwierigkeiten und theoretische und praktische Ansätze zur möglichen Lösung dieses sogenannten Tschebyscheff-Approximation-Problem, sind in (Kapitel 8.7.2, Richter and Wick 2017) gut nachzulesen.

9.1 Universal Approximation

Wir wollen hier nachvollziehen, dass klassische neuronale Netze, dieses Problem approximativ aber mit beliebiger Genauigkeit \(\epsilon\) lösen könnten. Die Schritte da hin sind wie folgt

  1. Zu einem gegebenen \(f\in \mathcal C[a, b]\) (einer reellwertigen, stetigen Funktion auf einem endlichen und abgeschlossenen Intervall) existiert immer eine stückweise konstante Funktion \(f_N\) mit endlich vielen Sprungstellen, sodass \[\begin{equation*} \|f-f_N\|_\infty < \frac \epsilon2 \end{equation*}\]

  2. Zu diesem \(f_N\) können wir immer eine Funktion \[\begin{equation*} s_M(x) = c_0 + \sum_{i=1}^Mc_i \tanh (a_i(x - b_i)) \end{equation*}\] konstruieren (durch Anpassung der Parameter \(c_0\), \(c_i\), \(b_i\), \(a_i\), \(i=1,\dotsc, M\)) sodass \[\begin{equation*} \|f_N-s_M\| < \frac \epsilon2. \end{equation*}\]

  3. Wir interpretieren \(s_M\) als ein neuronales Netz mit einer hidden layer und können konstatieren dass \[\begin{equation*} \|f-s_M\|_\infty \leq \|f-f_N\|_\infty + \|f_N-s_M\|_\infty < \frac \epsilon2 + \frac \epsilon2 = \epsilon. \end{equation*}\]

Einige Fragen werden wir unbeantwortet lassen müssen, vor allem

  • wie wählen wir \(M\) (das Resultat sagt nur \(M\) muss groß genug sein)

und

  • wie wirkt sich in der Praxis die approximative Berechnung von \(a_i\)–\(c_i\) auf die Approximation aus?

Dennoch gibt dieses Beispiel einen Einblick in die Funktionsweise der Approximation und das referenzierte universal approximation theorem ist Grundlage vieler Analyseansätze für neuronale Netzwerke.

In Schritt 1, wird die stückweise konstante Funktion \(f_N\) definiert. Die Existenz folgt aus dem Satz

Theorem 9.1 (Approximation durch stückweise konstante Funktionen) Sei \([a, b]\subset \mathbb R^{}\) ein abgeschlossenes endliches Intervall. Der Abschluss bezüglich der Supremumsnorm der Menge \(\operatorname{Pc}[a, b]\) aller stückweise konstanten Funktionen auf \([a, b]\) mit endlich vielen Sprungstellen enthält \(\mathcal C[a, b]\), d.h. \[\begin{equation*} \mathcal{C}[a, b]\subset \operatorname{closure}_{\|\cdot\|_\infty}(\operatorname{Pc}[a, b]). \end{equation*}\] Insbesondere, existiert für ein beliebiges \(f\in \mathcal C[a, b]\) und \(\varepsilon > 0\), immer ein \(g\in \operatorname{Pc}[a, b]\) mit \(\|f-g\|_\infty<\varepsilon\).

Proof. Der Beweis ist klassisch – hier nur die relevanten und konstruktiven Elemente.

An sich muss gezeigt werden, dass es zu jeder Funktion \(f\in \mathcal C[a, b]\) eine Folge \(\{f_n\}\subset \operatorname{Pc}[a, b]\) gibt, mit \(f\) als Grenzwert. Wir zeigen nur die Konstruktion eines potentiellen Folgengliedes.

Sei \(f\in \mathcal{C}[a, b]\) beliebig. Da stetige Funktionen auf kompakten Mengen gleichmäßig stetig sind, gibt es zu jedem \(\varepsilon>0\) ein \(\delta>0\), sodass \[\begin{equation*} |f(x\pm h) - f(x)| < \varepsilon \end{equation*}\] für alle \(h<\delta\). Damit können wir zu jedem \(\varepsilon\) eine Unterteilung von \((a, b]\) in \(N(\delta)\) halboffene (bis auf das abgeschlossene “erste” Intervall, das \(a\) enthält) disjunkte Intervalle \(I_j\), \(j=1, \dotsc, N(\delta)\) finden, sodass \[\begin{equation*} f_N(x) = \sum_{j=1}^N\chi_{I_j}(x) \end{equation*}\]

mit den Indikatorfunktionen \(\chi_{I_j}\) und mit \[\begin{equation*} f_j = \frac 12 (\max_{\xi\in I_j}\{f(\xi)\}+\min_{\eta \in I_j}\{f(\eta)\}) \end{equation*}\] eine Funktion aus \(\operatorname{PL}[a, b]\) darstellt, die um maximal \(\varepsilon\) von \(f\) abweicht. Außerdem können wir damit sicherstellen, dass \(j=1, \dotsc, N-1\) gilt, was im nächsten Schritt relevant wird.

In Schritt 2 wird nun die Funktion \(f_N\) durch Linearkombinationen von transformierten \(\tanh\) Funktionen approximiert: \[\begin{equation*} f_N(x) \approx g_M(x) := c_0 + \sum_{i=1}^Mc_i\tanh(a_i(x-b_i)) \end{equation*}\]

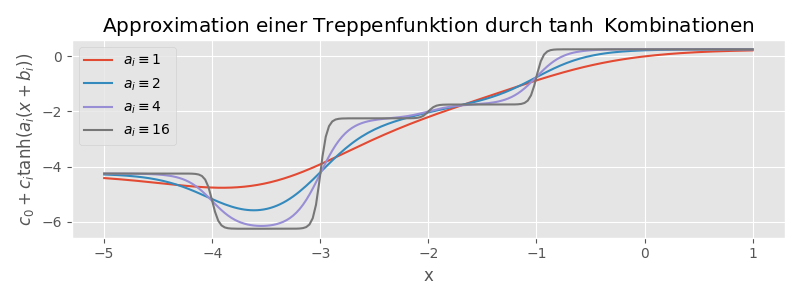
Beispiel Illustration wie eine Linearkombination von skalierten \(\tanh\) Funktionen eine Treppenfunktion approximiert

Die Konstruktion und der Nachweis, dass für jedes \(\varepsilon<0\) (mit \(f_N\) bereits entsprechend konstruiert) eine Differenz \(\|f_N - g_M\|_\infty < \varepsilon\) möglich ist, basiert auf folgenden Argumenten:

  • Allgemein gilt für die Funktion \(\tanh\), dass sie streng monoton ist, dass \(\tanh(0)=0\) und dass \(\lim_{x\to \pm \infty} \tanh(x) = \pm 1\).

  • Durch eine Skalierung von \(x\leftarrow ax\) mit \(a\to \infty\), passiert der übergang von \(-1\) zu \(1\) beliebig schnell – \(\tanh\) entspricht zunehmend der Treppenfunktion, die bei \(0\) von \(-1\) auf \(+1\) springt. (Jan bemerke, dass diese “Konvergenz” nicht bezüglich der Supremumsnorm stattfindet.)

  • Durch einen Shift \(x \leftarrow x-b\) kann der Sprung von \(x=0\) zu \(x=b\) verschoben werden.

  • Durch Skalierung \(\tanh \leftarrow c\tanh\) kann die Höhe des Sprungs angepasst werden.

Damit (und insbesondere mit \(b_i\) als die Sprungstellen von \(f_N\) gewählt und \(c_i\) als die Differenz zwischen den Werten an diesem Sprung), kann direkt ein \(g_M\) konstruiert werden, das bis auf beliebig kleine, offene Umgebungen um die Sprungstellen dem \(f_N\) beliebig nahe kommt. (Allerdings nicht in der Supremumsnorm). Da für genügend große \(a_i\) aber sichergestellt wird, dass \(g_M\) auf jedem Teilintervall zwischen den Werten von \(f_N\) interpoliert, folgt aus (9.1), dass auch die punktweise Differenz kleiner als \(\varepsilon\) ist. Insgesamt folgt so die Existenz von \(g_M\) mit den gewünschten Eigenschaften.

Im letzten Schritt 3 interpretieren wir die \(g_M\) Approximation als ein neuronales Netz.

Dazu bemerken wir, dass wir \(g_M\) schreiben können als \[\begin{equation*} c= \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_M \end{bmatrix}, \quad A= \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_M \end{bmatrix}, \quad b= \begin{bmatrix} -a_1b_1 \\ -a_2b_2 \\ \vdots \\ -a_Mb_M \end{bmatrix} \end{equation*}\] und der eintragsbezogenen Interpretation der eigentlich skalaren \(\tanh\) Funktion und dass

  • der Anteil \[\begin{equation*} \tanh (Ax+b) \end{equation*}\] eine klassische linear layer mit Aktivierung ist
  • während der Ausgang \(y=c_0+c^T\xi\) eine einfache lineare Abbildung (ohne Aktivierung ist).

In dieser Darstellung, ist die Suche nach den Parametern für \(g_M\) in den Standardroutinen von ML Paketen ohne weiteres möglich.

Wir schließen mit einigen allgemeinen Bemerkungen

  • die Funktion \(\tanh\) hat durchaus Relevanz in der Praxis. Für die Theorie, die im wesentlichen Beschränktheit und Monotonie voraussetzt, gehen auch die gerne verwendeten allgemeineren sigmoid Funktionen.
  • die größte Lücke zur Praxis ist die Annahme \(M\) genügend groß. Etwas unpraktisch ist auch, dass nur eine hidden layer verwendet wird. Neuere Arbeiten behandeln ähnliche Approximationsresultate mit mehreren Schichten.
  • die theoretisch unschönste Lücke ist die Annahme, dass eine Funktion auf einer kompakten Menge approximiert wird (was beispielsweise in der Behandlung von dynamischen Systemen nachteilig ist)
  • Zur Approximation von \(f_N\) ist Jan geneigt, die \(a_i\) einfach sehr groß zu wählen. Ist \(f\) stetig, dann werden allerdings bessere Resultate (die den Verlauf von \(f\) nachzeichnen) mit kleineren \(a_i\) erreicht. Außerdem führen große Werte von \(a\) zum sogenannten vanishing gradients Phänomen, da \(\frac{\tanh(a(x+h))-\tanh(ax)}{h}\to 0\) für \(a\to \infty\).

9.2 Aufgaben

Zur Approximation einer Funktion \(f\colon \mathbb R^{}\to \mathbb R^{}\) über den Ansatz (9.2) seien Datenpunkte \(\mathbb X = \{(x_i, y_i)\}_i\) mit \(y_i=f(x_i)\) gegeben und das Optimierungsproblem \[\begin{equation*} L(c, A, b; \mathbb X) = \sum_{i} \|y_i - g_M(c, A, b;\, x_i)\|_2^2 \to \min_{c, A, b} \end{equation*}\] mittels des stochastischen Gradientenabstiegs zu lösen.

  1. Schreiben Sie die Koeffizienten in einen Vektor \(p=(c, A, b)\) und berechnen Sie \(\nabla_{c_0}L(p; \mathbf x)\), sowie beispielhaft die Komponenten von \(\nabla_p L(p; \mathbf x)\) für einen einzelnen Datenpunkt \(\mathbf x = x_i\) oder einen batch \(\mathbf x = \mathbb x\) (wie es für den stochastischen Gradienten benutzt würde).

  2. Formulieren Sie die Berechnung des Gradienten (bezüglich \(p\)) für \(M=1\) und einen Datenpunkt \(x\), also für die Funktion \(l = L(c_0, c_1, a_1, b_1; x)\) über automatisches Differenzieren im Vorwärts– und im Rückwärtsmodus.

  3. Implementieren Sie die Approximation und das Training. Dafür können die Bausteine aus Beispiel Implementierung verwendet werden. Implementieren Sie auch die Gradientenberechnung zur Verwendung im stochastischen Abstiegsverfahren. Testen Sie ihre Implementierung für verschiedene \(M\) und verschiedene Daten für die Funktionen \[\begin{equation*} f_1(x)=\chi_{[-1, 0]}(x) - \chi_{(0, \frac 13]}(x)+ \chi_{(\frac 13, \frac 12]}(x) - \chi_{(\frac 12, 1]}(x), \quad f_2(x) = \sin(4x) \end{equation*}\] jeweils auf dem Intervall \([-1, 1]\).

Referenzen

Richter, T., Wick, T.: Einführung in die numerische Mathematik. Begriffe, Konzepte und zahlreiche Anwendungsbeispiele. Heidelberg: Springer Spektrum (2017)

  1. für ein kompaktes Intervall wird das zur Maximumsnorm↩︎