6 Singulärwert Zerlegung

Die Singulärwertzerlegung ist ein Universalwerkzeug der Datenanalyse und Modellsynthese. Die wesentliche Eigenschaft ist die Quantifizierung wesentlicher und redundanter Anteile in Daten oder Operatoren.

Die direkte Anwendung ist die Principal Component Analysis, die orthogonale Dimensionen in multivariablen Daten identifiziert, die nach der Stärke der Varianz sortiert sind. So kann diese erste principal component als die reichhaltigste Datenrichtung interpretiert werden und die letzten Richtungen (insbesondere wenn die Varianz komplett verschwindet) als wenig aussagekräftig (und insbesondere redundant) identifiziert werden.

Andere Anwendungen ist die Lösung von überbestimmten Gleichungssystemen (wie sie in der linearen Regression vorkommen) oder das Entfernen von Rauschen aus Daten.

6.1 Definition und Eigenschaften

Theorem 6.1 (Singulärwertzerlegung (SVD)) Sei $A\in \mathbb C^{m\times n}$, $m\geq n$. Dann existieren orthogonale Matrizen $U \in \mathbb C^{m\times m}$ und $V\in \mathbb C^{n\times n}$ und eine Matrix $\Sigma \in \mathbb R^{m\times n}$ der Form \[\begin{equation*} \Sigma = \begin{bmatrix} \sigma_1 & 0 & \dots & 0\\ 0 & \sigma_2 &\ddots & \vdots\\ 0 & \ddots & \ddots &0\\ 0 & \dots&0 & \sigma_n \\ 0 & 0 & \dots & 0 \\ \vdots & \ddots & & \vdots\\ 0 & 0 & \dots & 0 \end{bmatrix} \end{equation*}\] mit reellen sogenannten Singulärwerten \[\begin{equation*} \sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_n \geq 0 \end{equation*}\] sodass gilt \[\begin{equation*} A = U \Sigma V^* \end{equation*}\] wobei gilt $V^* = \overline{V^T}$ (transponiert und komplex konjugiert).

Ein paar Bemerkungen.

Ist $A$ reell, können auch $U$ und $V$ reell gewählt werden.
Ein Beweis ist in (Bollhöfer and Mehrmann 2004, Satz 14.14) zu finden.
Die Annahme $m \geq n$ war nur nötig um für die Matrix $\Sigma$ keine Fallunterscheidung zu machen. (Für $m\leq n$ “steht der Nullblock rechts von den Singulärwerten”). Insbesondere gilt $A^* = V\Sigma U^*$ ist eine SVD von $A^*$.
Eine Illustration der Zerlegung ist Abbildung 6.1 zu sehen.

Wir machen einige Überlegungen im Hinblick auf große Matrizen. Sei dazu $m>n$, $A\in \mathbb C^{m\times n}$ und $A=U\Sigma V^*$ eine SVD wie in Theorem 6.1. Sei nun \[\begin{equation*} U = \begin{bmatrix} U_1 & U_2 \end{bmatrix} % = \begin{bmatrix} V_1^* & V_2^* \end{equation*}\] partitioniert sodass $U_1$ die ersten $n$ Spalten von $U$ enthält.

Dann gilt (nach der Matrix-Multiplikations Regel Zeile mal Spalte die Teile $U_2$ und $V_2$ immer mit dem Nullblock in $\Sigma$ multipliziert werden) dass \[\begin{equation*} A = U\Sigma V = \begin{bmatrix} U_1 & U_2 \end{bmatrix} \begin{bmatrix} \hat \Sigma \\ 0 \end{bmatrix} V^* % \begin{bmatrix} V_1^* \\ V_2^* \end{bmatrix} = U_1 \hat \Sigma V^* % \begin{bmatrix} V_1^* \\ V_2^* \end{bmatrix} \end{equation*}\] Es genügt also nur die ersten $m$ Spalten von $U$ zu berechnen. Das ist die sogenannte slim SVD.

Hat, darüberhinaus, die Matrix $A$ keinen vollen Rang, also $\operatorname{Rg}(A) = r < n$, dann:

ist $\sigma_i=0$, für alle $i=r+1, \dotsc, n$, (wir erinnern uns, dass die Singulärwerte nach Größe sortiert sind)
die Matrix $\hat \Sigma$ hat $n-r$ Nullzeilen
für die Zerlegung sind nur die ersten $r$ Spalten von $U$ und $V$ relevant – die sogenannte Kompakte SVD.

In der Datenapproximation ist außerdem die truncated SVD von Interesse. Dazu sei $\hat r<r$ ein beliebig gewählter Index. Dann werden alle Singulärwerte, $\sigma_i=0$, für alle $i=\hat r+1, \dotsc, n$, abgeschnitten – das heißt null gesetzt und die entsprechende kompakte SVD berechnet.

Hier gilt nun nicht mehr die Gleichheit in der Zerlegung. Vielmehr gilt \[\begin{equation*} A \approx A_{\hat r} \end{equation*}\] wobei $A_{\hat r}$ aus der truncated SVD von $A$ erzeugt wurde. Allerdings ist diese Approximation von $A$ durch optimal in dem Sinne, dass es keine Matrix vom Rang $\hat r \geq r=\operatorname{Rg}(A)$ gibt, die $A$ (in der induzierten euklidischen Norm) besser approximiert. Es gilt \[\begin{equation*} \min_{B\in \mathbb C^{m\times n}, \operatorname{Rg}(B)=\hat r} \|A-B\|_2 = \|A-A_{\hat r}\|_2 = \sigma_{\hat r + 1}; \end{equation*}\] (vgl. Satz 14.15, Bollhöfer and Mehrmann 2004).

Zum Abschluss noch der Zusammenhang zur linearen Ausgleichsrechnung. Die Lösung $w$ des Problems der linearen Ausgleichsrechnung war entweder als Lösung eines Optimierungsproblems \[\begin{equation*} \min_{w} \| Aw - y \|^2 \end{equation*}\] oder als Lösung des linearen Gleichungssystems \[\begin{equation*} A^TAw=y. \end{equation*}\] Ist $A=U\Sigma V^*=U_1\hat \Sigma V^*$ (slim) “SV-zerlegt”, dann gilt \[\begin{equation*} A^*Aw = V\hat \Sigma^*U_1^*U_1\hat \Sigma V^*w = V\hat \Sigma^2 V^* w \end{equation*}\] und damit \[\begin{equation*} A^*Aw = A^*y \quad \Leftrightarrow \quad V\hat \Sigma^2 V^*w = V\hat \Sigma^*U_1^*y \quad \Leftrightarrow \quad w = V\hat \Sigma^{-1} U_1^*y \end{equation*}\] was wir (mit den Matrizen der vollen SVD) als \[\begin{equation*} w = V \Sigma^+ U^*y \end{equation*}\] schreiben, wobei \[\begin{equation*} \Sigma^+ = \begin{bmatrix} \hat \Sigma^{-1} \\ 0_{m-n \times n} \end{bmatrix} \end{equation*}\] .

Bemerkung: $\Sigma^+$ kann auch definiert werden, wenn $\hat \Sigma$ nicht invertierbar ist (weil manche Diagonaleinträge null sind). Dann wird $\hat \Sigma^+$ betrachtet, bei welcher nur die $\sigma_i>0$ invertiert werden und die anderen $\sigma_i=0$ belassen werden. Das definiert eine sogenannte verallgemeinerte Inverse und löst auch das Optimierungsproblem falls $A$ keinen vollen Rang hat.

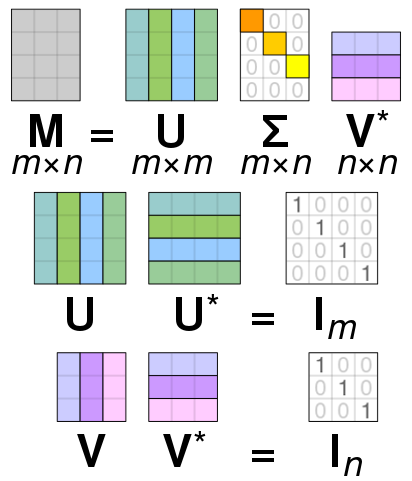
Illustration der SVD. Bitte beachten, der $*$ bedeutet hier transponiert und komplex konjugiert. By Cmglee - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=67853297

Figure 6.1: Illustration der SVD. Bitte beachten, der $*$ bedeutet hier transponiert und komplex konjugiert. By Cmglee - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=67853297

6.2 Numerische Berechnung

Die praktische Berechnung der Singulärwertzerlegung einer Matrix $A\in \mathbb R^{m\times n}$ verlangt einen gesamten Grundkurs in numerischer Mathematik.

In direkter Weise könnten die Singulärwerte und –vektoren über das Eigenwertproblem für $AA^T$ oder $A^TA$ bestimmt werden. Das ist nicht so schlecht, wie mit dem Argument, dass sich mit dem quadrieren der Matrizen auch die Konditionszahl quadriert, gerne nahegelegt wird,³ da

wenn $n\ll m$ oder $m\ll n$, dann ist $A^TA$ oder $AA^T$ wesentlich kleiner als $A$
das Eigenwertproblem symmetrisch ist, was gut ausgenutzt werden kann
wenn $A$ sehr gross aber dünnbesetzt (engl. sparse) ist, dann können die Eigenwerte durch effiziente sparse matrix-vector Multiplikationen angenähert werden
es können ohne weiteres nur eine Anzahl von Singulärwerten berechnet werden

sodass für sparse Matrizen diese Methode der de-facto Standard ist⁴.

Für normale Matrizen kommt jedoch der folgende Algorithmus, der mehrere wunderbar effiziente Algorithmen elegant kombiniert besser in Betracht:

Betrachte \[M=\begin{bmatrix} 0 & A \\ A^T & 0 \end{bmatrix} \in \mathbb R^{n+m \times n+m},\] deren positiven Eigenwerte mit den (positiven) Singulärwerten von $A$ übereinstimmen.
Bringe $M$ durch Householder transformationen in Hessenberg-Form, also \[ H = QMQ^T \] mit $Q$ orthogonal. Wegen Orthogonalität ist das eine Ähnlichkeitstransformation ($H$ hat die gleichen Eigenwerte wie $M$) und wegen Symmetrie von $M$ ist auch $H$ symmetrisch und damit tridiagonal.
Berechne die positiven Eigenwerte von $H$ mittels der QR-Iteration, die für Hessenbergmatrizen sehr effizient implementiert werden kann.

Der Standard⁵ funktioniert wie folgt:

Berechne eine orthogonale Transformation auf eine bidiagonale $B=U_A^TAV_A$.
Berechne eine SVD von $B=U_B\Sigma V_B^T$ (das wird effizient mit einem divide and conquer Algorithmus von Gu und Eisenstat getan)
Erhalte die gesuchte SVD als $A=(U_AU_B)\Sigma (V_AV_B)^T$.

6.3 Aufgaben

6.3.1 Norm und Orthogonale Transformation

Sei $Q\in \mathbb R^{n\times n}$ eine orthogonale Matrix und sei $y\in \mathbb R^{n}$. Zeigen Sie, dass \[\begin{equation*} \|y\|^2 = \|Qy \|^2 \end{equation*}\] gilt.

6.3.2 Kleinste Quadrate und Mittelwert

Zeigen sie, dass der kleinste Quadrate Ansatz zur Approximation einer Datenwolke \[\begin{equation*} (x_i, y_i), \quad i=1,2,\dotsc,N, \end{equation*}\] mittels einer konstanten Funktion $f(x)=w_1$ auf $w_1$ auf den Mittelwert der $y_i$ führt.

6.3.3 QR Zerlegung und Kleinstes Quadrate Problem

Sei $A\in \mathbb R^{m,n}$, $m>n$, $A$ hat vollen Rank und sei \[\begin{equation*} \begin{bmatrix} Q_1 & Q_2 \end{bmatrix} \begin{bmatrix} \hat R \\ 0 \end{bmatrix} = A \end{equation*}\] eine QR-Zerlegung von $A$ (d.h., dass $Q$ unitär ist und $\hat R$ eine (im Falle, dass $A$ vollen Rang hat invertierbare) obere Dreiecksmatrix. Zeigen sie, dass die Lösung von \[\begin{equation*} \hat R w = Q_1^T y \end{equation*}\] ein kritischer Punkt (d.h. der Gradient $\nabla_w$ verschwindet) von \[\begin{equation*} w \mapsto \frac 12 \| Aw - y \|^2 \end{equation*}\] ist, also $w=\hat R^{-1}Q_1^T y$ eine Lösung des Optimierungsproblems darstellt. Vergleichen Sie mit der SVD Lösung aus der Vorlesung.

6.3.4 Eigenwerte Symmetrischer Matrizen

Zeigen Sie, dass Eigenwerte symmetrischer reeller Matrizen $A\in \mathbb R^{n\times n}$ immer reell sind.

6.3.5 Singulärwertzerlegung und Eigenwerte I

Zeigen Sie, dass die quadrierten Singulärwerte einer Matrix $A\in \mathbb R^{m\times n}$, $m>n$, genau die Eigenwerte der Matrix $A^TA$ sind und beschreiben Sie in welcher Beziehung sie mit den Eigenwerten von $AA^T$ stehen. Hinweis: hier ist “$m>n$” wichtig.

6.3.6 Singulärwertzerlegung und Eigenwerte II

Weisen Sie nach, dass die positiven Eigenwerte von \[\begin{equation*} \begin{bmatrix} 0 & A^T \\ A & 0 \end{bmatrix} \end{equation*}\] genau die nicht-null Singulärwerte von $A$ sind.

6.3.7 Truncated SVD

Berechnen und plotten sie die Singulärwerte einer $4000\times 1000$ Matrix mit zufälligen Einträgen und die einer Matrix mit “echten” Daten (hier Simulationsdaten einer Stroemungssimulation)⁶. Berechnen sie den Fehler der truncated SVD $\|A-A_{\hat r}\|$ für $\hat r = 10, 20, 40$ für beide Matrizen.
Was lässt sich bezüglich einer Kompression der Daten mittels SVD für die beiden Matrizen sagen. (Vergleichen sie die plots der Singulärwerte und beziehen sie sich auf die gegebene Formel für die Differenz).
Für die “echten” Daten: Speichern sie die Faktoren der bei $\hat r=40$ abgeschnittenen SVD und vergleichen Sie den Speicherbedarf der Faktoren und der eigentlichen Matrix.

Beispielcode:

import numpy as np
import scipy.linalg as spla
import matplotlib.pyplot as plt

randmat = np.random.randn(4000, 1000)

rndU, rndS, rndV = spla.svd(randmat)

print('U-dims: ', rndU.shape)
print('V-dims: ', rndV.shape)
print('S-dims: ', rndS.shape)

plt.figure(1)
plt.semilogy(rndS, '.', label='Singulaerwerte (random Matrix)')

realdatamat = np.load('velfielddata.npy')

# # Das hier ist eine aufwaendige Operation
rlU, rlS, rlV = spla.svd(realdatamat, full_matrices=False)
# # auf keinen Fall `full_matrices=False` vergessen

print('U-dims: ', rlU.shape)
print('V-dims: ', rlV.shape)
print('S-dims: ', rlS.shape)

plt.figure(1)
plt.semilogy(rlS, '.', label='Singulaerwerte (Daten Matrix)')

plt.legend()
plt.show()

Hinweis: Es gibt viele verschiedene Normen für Vektoren und Matrizen. Sie dürfen einfach mit np.linalg.norm arbeiten. Gerne aber mal in die Dokumentation schauen welche Norm berechnet wird.

Referenzen

Bollhöfer, M., Mehrmann, V.: Numerische Mathematik. Eine projektorientierte Einführung für Ingenieure, Mathematiker und Naturwissenschaftler. Vieweg (2004)

Richter, T., Wick, T.: Einführung in die numerische Mathematik. Begriffe, Konzepte und zahlreiche Anwendungsbeispiele. Heidelberg: Springer Spektrum (2017)

denn die Kondition des Eigenwertproblems ist direkt proportional zur Kondition der Matrix; vgl. (Satz 5.9, Richter and Wick 2017)↩︎
und beispielsweise die Methode, die in scipy.sparse.linalg.svd implementiert ist↩︎
z.B. die LAPACK routinen, die die Basis bspw. von numpy.linalg.svd aber auch von Matlab’s SVD ist↩︎
Download bitte hier – Achtung das sind 370MB↩︎